分子軌道を得るには量子化学計算ソフトやプログラミングが必要と思っている方もいるのではないでしょうか?
ご存じの方も多いですが、永年方程式を解くことでエチレンや1,3ブタジエンのπ軌道を簡単に調べることができます。しかし、π軌道がなぜ永年方程式で得ることができるか考えたことはありますか?
このページではπ電子に対象を絞ったヒュッケル法とすべての電子に対して量子計算を行うRHF法を比べることで、ヒュッケル法(永年方程式)でπ軌道が得られる秘密にせまります。
- ヒュッケル法で分子軌道を得る手続きを再確認する
- RHF法と永年方程式の類似点を確認する。

ヒュッケル法でエチレンのπ軌道を得る
実は、ヒュッケル法でエチレンのπ軌道がきれいに得られる理由は簡単です。
エチレンが平面構造になっているため、原子軌道の$xy$平面成分と$z$軸成分が相互作用しないためです。

最終的にはRHF法の結果からこの事実を確認しますが、まずはヒュッケル法でエチレンのπ軌道を求めてみましょう。
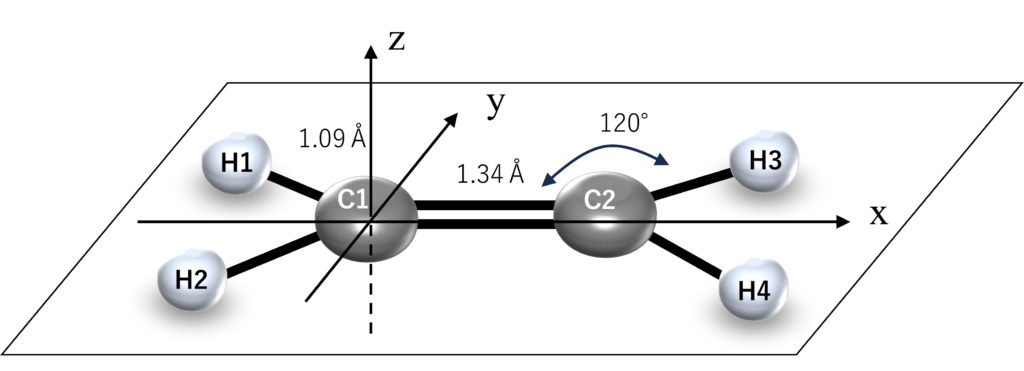
永年方程式は以下のヒュッケル近似を利用するとつくることができます。
- すべての重なり積分を$0$とする。
- 隣接しない原子間の共鳴積分$\beta$は$0$
- すべての共鳴積分$\beta~~(<0)$は等しい
永年方程式の丁寧な導出はこちら
まずは求めるエチレンのπ軌道を$\Psi$とし、$\Psi$がエチレンの炭素原子1と2のpz軌道$\phi_1$と$\phi_2$の線形和で表されるとします。
つまりエチレンのπ軌道$\Psi$が次の形で表されるとします。
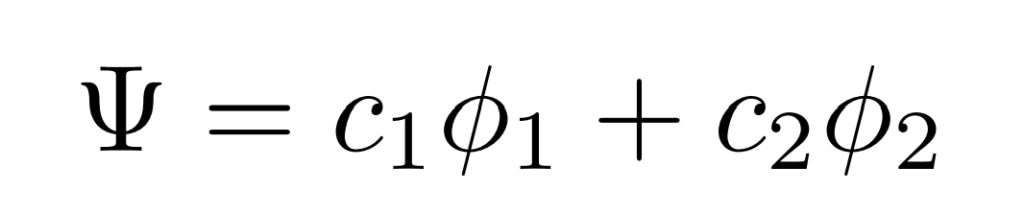
次にこの分子軌道$\Psi$のエネルギー$E$の標識を求めます。エネルギー$E$は系のハミルトニアン$\hat{H}$を用いて$E=\int\Psi\hat{H}\Psi$で求められます。
この$E$の標識を得るために、クーロン積分$\alpha$と共鳴積分$\beta$を導入します。
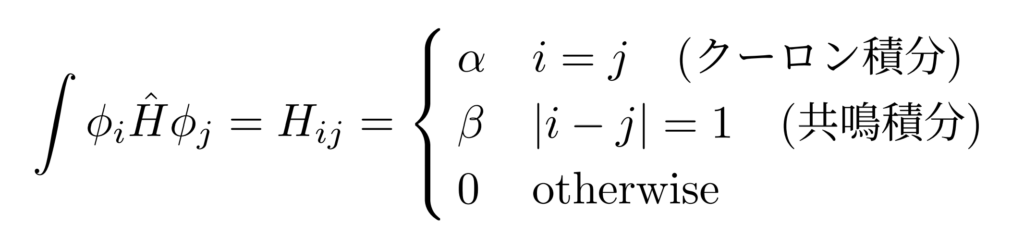
このクーロン積分$\alpha$と共鳴積分$\beta$を利用するとエネルギー$E=\int\Psi\hat{H}\Psi$は次の形で表現できることがわかります。
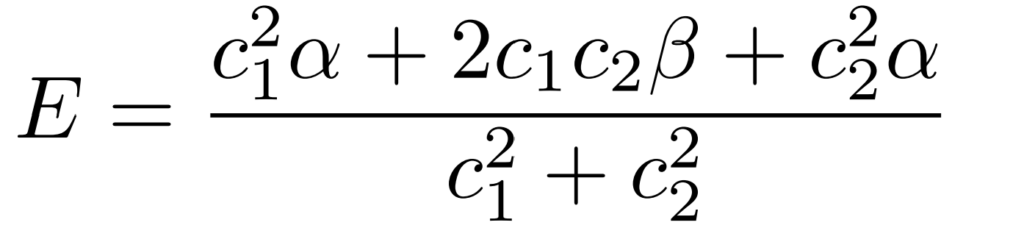
このエネルギー$E$が最小値(極小値)となる条件は次です。
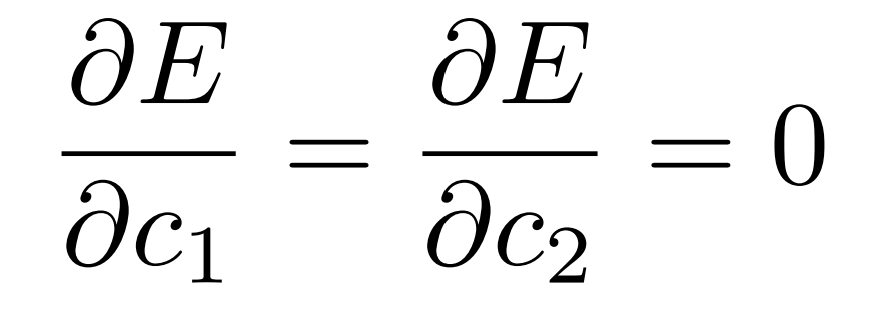
この条件を整理すると、次の固有値方程式を解けば最小のエネルギーを与える$c_1$、$c_2$とその時のエネルギー$E$を求めることができます。
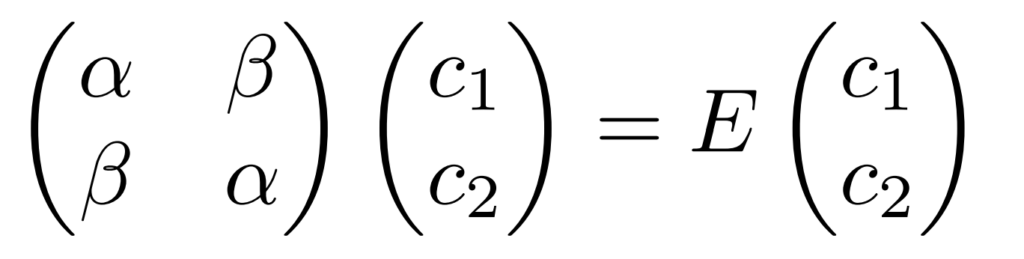
この固有値方程式を解く方法として、行列式が$0$となる条件がよく用いられ、この表式をHuckel法の解法としてみたことがあるひとが多いのではないでしょうか。
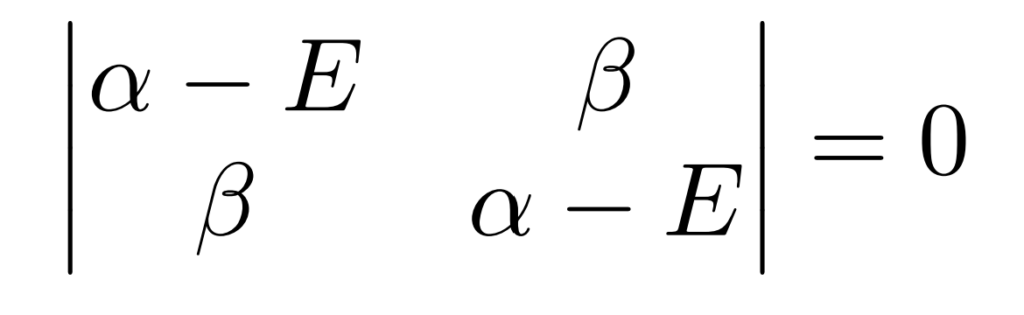
これを解くと$E$が求められ、$c_1$と$c_2$の組も自動的に求めることができます。
エチレンのヒュッケル法では、次の行列の固有値問題方程式を解けば分子軌道の係数$c_1$、$c_2$とその時のエネルギー$E$を求めることができます。
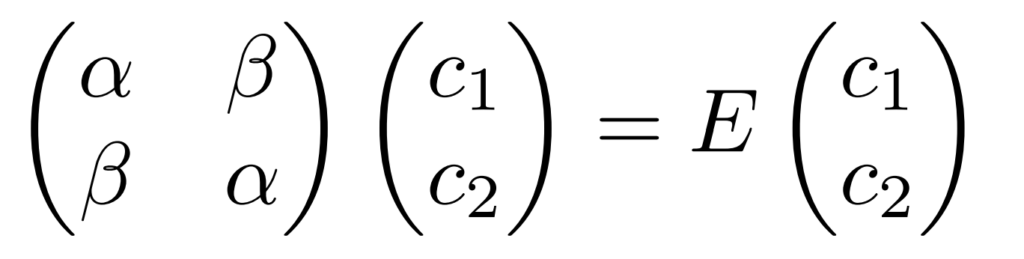
この固有値方程式を解く方法として、行列式が$0$となる条件がよく用いられます。
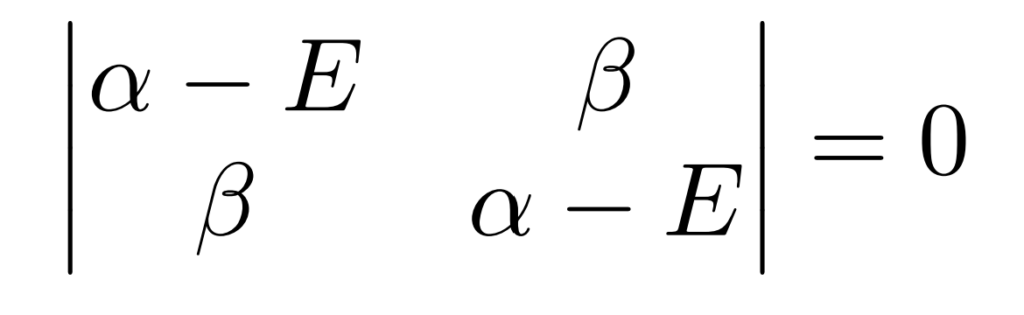

これが永年方程式だよね。
これを解いた結果が↓の図です。高エネルギーの軌道はエチレンのp軌道が逆位相になり、低エネルギーの軌道は同位相になります。
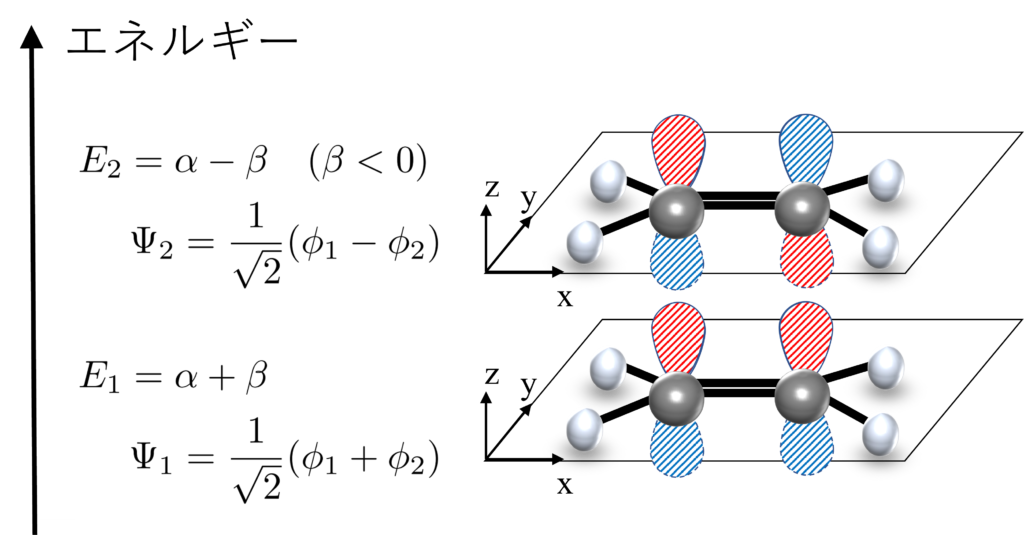

低エネルギー軌道は同位相で、高エネルギー軌道は逆位相ですね。
以上がエチレンのπ軌道をHuckel法で解くときの方法です。
つぎにこのHuckel法はエチレンのπ軌道を求めるだけの方法でしたが、全電子の軌道を求めるRHF法と比較してみます。
RHF法による量子化学計算は何をしているか

さて、ここからが本番です。
ヒュッケル法でエチレンのπ軌道がきれいに得ることができる秘密を知るために、RHF法(全ての軌道を計算)で分子軌道を得る手続きを紹介します。
RHF法では分子軌道の組$\boldsymbol{C}$を変えながら電子状態のエネルギーの計算を行い、最終的な分子軌道を得ます。

RHF法では繰り返し(ループ)計算を使って、分子軌道を得るんだね。
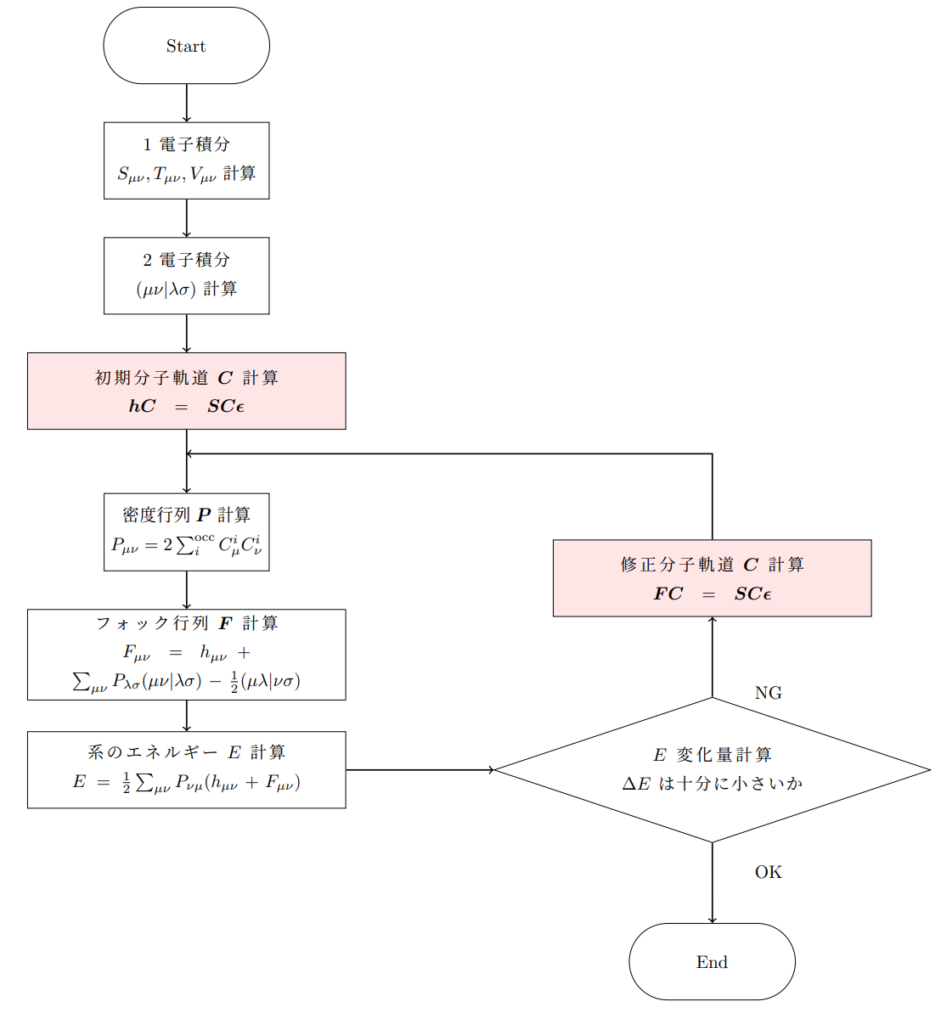

Huckel法とRHF法を比較するため、RHF法のフローチャートの赤色塗りつぶし部に着目していきましょう。
RHF法ではエチレンの行列はブロック状になります
1電子積分から得られるハミルトニアン$h$を確認
行列の固有値方程式$\boldsymbol{hC}=\boldsymbol{SC\epsilon}$を解くことで最も簡単な分子軌道を得ることができます

つまり、初期の分子軌道$\boldsymbol{C}$は$\boldsymbol{(S^{-1}h)C}=\boldsymbol{\epsilon{C}}$を解くと得られるんだね。

この$\boldsymbol{h}$では電子間反発を考慮していません
この$\boldsymbol{(S^{-1}h)}$の行列を確認してみましょう。これを対角化すると分子軌道$\boldsymbol{C}$が得られます。
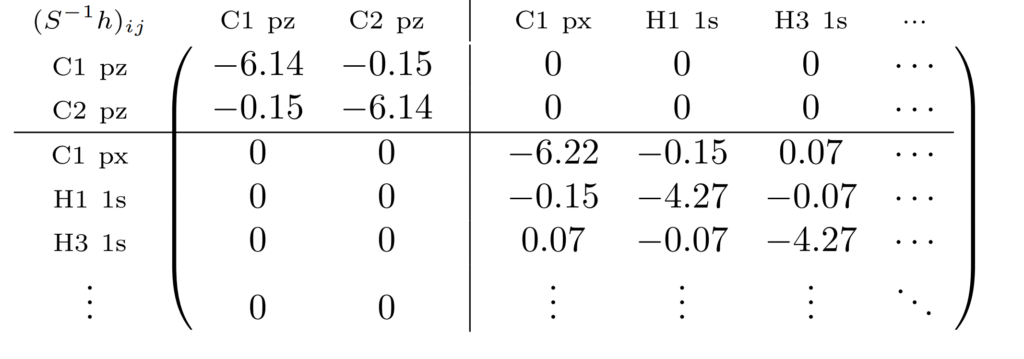
確認すると、対角化する行列はC1とC2のpz部分とそれ以外でブロック構造になっていることがわかります。

行列の右上部分や左下部分はなぜ全部$0$なの?

エチレンが平面構造になっているため、軌道の$xy$平面成分と$z$成分との相互作用がすべて$0$になるためです。
結局、pz部分だけで考えると、次の固有値方程式を解くことになります。
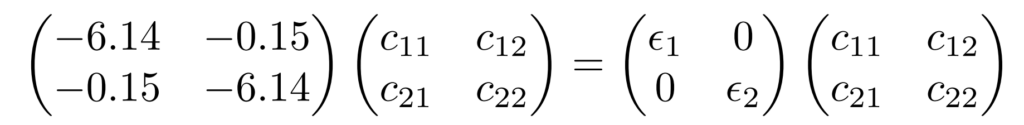
この方程式はHuckel法で解いたときクーロン積分$\alpha$を$-6.14$、共鳴積分$\beta$を$-0.15$としたときの方程式と一致します。

しっかりと$\beta<0$となっている点も注目です。
つまり、Huckel法はRHF法でpz成分がブロック分割できる(C1 pzとC1 pxやH3 1sなどの成分が$0$となる)こと利用して、エチレンのpz軌道をうまく得ているということができます。

エチレンが平面構造であることがヒュッケル法でπ軌道を得ることができる秘密なんだね。
収束時のフォック演算子$F$を確認
念のため、繰り返し計算が終わる際の$\boldsymbol{(S^{-1}F)}$も確認しておきましょう。↑のフローチャートの右赤塗りつぶし部分の行列です。

結果、$\boldsymbol{(S^{-1}h)}$と同じようにブロック行列の形になっていることが確認できました。しかし、クーロン積分$\alpha$の値は$-0.15$と、$\boldsymbol{(S^{-1}h)}$のとき($-6.14$)よりかなり大きくなっています。

これは電子-電子反発の効果を取り入れたことにより安定化エネルギーが小さくなっているからと考えられます。
まとめ
Huckel法とRHF法で整合性がとれていることがわかりましたでしょうか。
Huckel法は解く対象をエチレンなどの平面外の軌道に絞ることでそのほかの原子軌道との相互作用を考えなくてよいことを利用し、簡単にπ軌道を得ているのです。