スレーター行列式は電子状態を表す重要な方法ですが、聞いたことがあっても、量子化学計算で実際にどのように使うかは知らない人も多いと思います。
スレーター行列式は扱う電子の数$N$が増えると爆発的な数($N!$個)の項が発生するという特徴がありますが、なぜそのようなスレーター行列式を使う必要があるのでしょうか?また、そのような大量の項の足し合わせは実際に計算できるのでしょうか?
このページでは、スレーター行列式を用いる理由と、実は量子化学計算(例えばプログラミング)する最終的な表式はシンプルになり、$N!$個もの足し合わせは必要ないことを紹介します。
- スレーター行列式が表す電子状態と分子軌道の違いを確認します
- スレーター行列式を使う必要性を解説します
- 実際の量子化学計算では大量の項の足し合わせは不要であることを解説します。

分子軌道と電子状態の違い
スレーター行列式(スレイター行列式、Slater行列式)は電子状態を表すために用いますが、この電子状態と分子軌道は何が違うか知っていますか?まずはこの2つの違いを確認していきましょう。
まず、「分子軌道」とはHOMOやLUMOなど、電子が入る対象のことを意味しており、よく小文字を使って$\chi$、$\phi$や$\psi$などで表されます。
一方、「電子状態」(全波動関数と呼ばれることもあります)は基底状態や励起状態など分子軌道にどのように電子が入っているかの状態を指しており、よく大文字を使って$\Phi$や$\Psi$などで表されます。
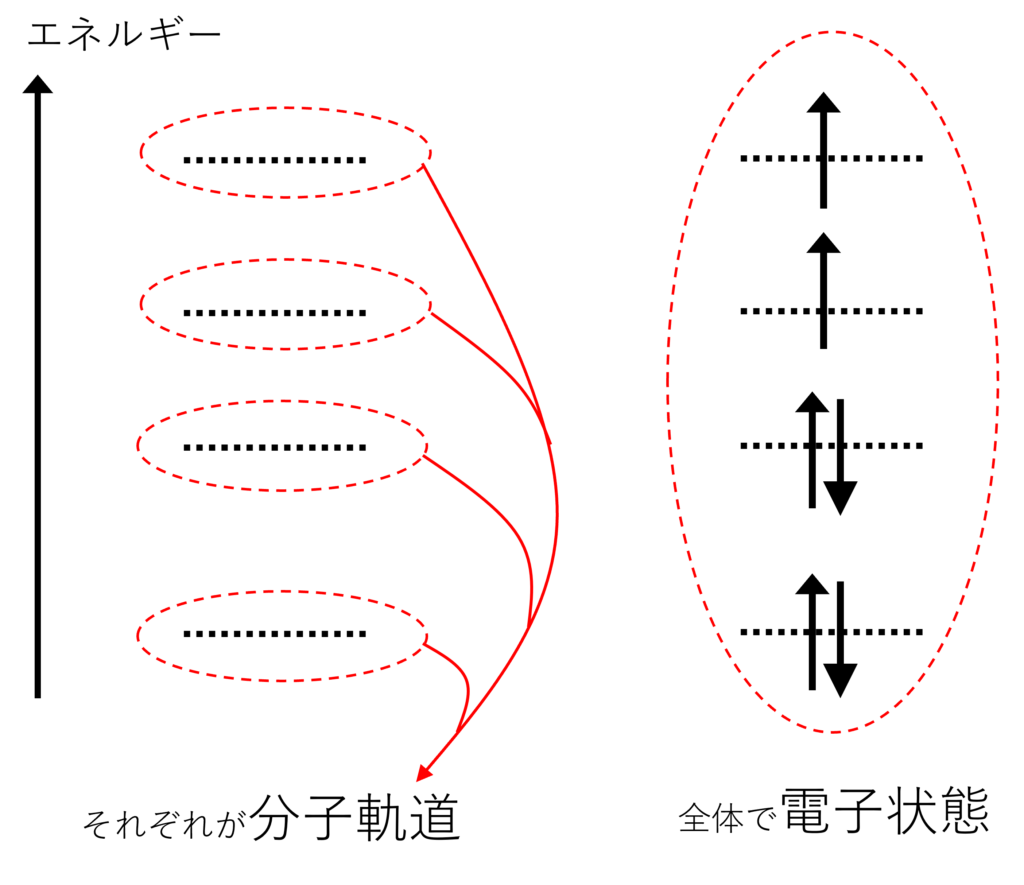
この電子状態を表すために使うのがスレーター行列式です。$N$個の電子が$N$個の軌道$\{\chi_i\}$に入るときの電子状態(全波動関数)$\Phi$を$\Phi=\frac{1}{\sqrt{N!}}\begin{vmatrix}\chi_1(x_1)&\cdots&x_N(x_1)\\\vdots&\ddots&\vdots\\\chi_1(x_N)&\cdots&\chi_N(x_N)\end{vmatrix}$と行列式を用いて表します。
行列式を書くのは大変なので、軌道だけを使って$\Phi=\ket{\chi_1,{\cdots},\chi_N}$と簡略化して書くこともあります。

あくまでも簡略化して表記しているだけで、中身はあくまでも行列式です。
スレーター行列式の特徴の1つは電子数が増えると爆発的に項数が増える点です。水素分子などの2電子系においては$2!=2$項の足し算、LiH等の4電子系においては$4!=24$項、水やメタン等の10電子系では$10!=3628800$項が必要になります。量子化学計算を行う上では、これら膨大な項数の和によって与えられる電子状態のエネルギーなどを求める必要があります。

実際の量子化学計算では、そんな大量の足し合わせを行う必要があるの?

後で解説しますが、電子エネルギーなどの最終的な表式ではかなりすっきり与えられます。
スレーター行列式を使う理由
なぜ項数が多いスレーター行列式を使って電子状態を表さなければならないのでしょうか?ここでは電子状態を$\Psi=\chi_1(x_1){\cdots}\chi_N(x_N)$(これはハートリー積と呼ばれるものです)としたときの問題点をお伝えします。
問題点:電子を区別してしまっている
ハートリー積を用いる問題点の1つは電子1が軌道$\chi_1$に入る、電子2が軌道$\chi_2$に入る、、、という風に電子を区別してしまっている点です。
しかし、電子は区別できません。電子はすべて同じ質量、電荷をもつためです。

スレーター行列式ではどのようにして電子が区別できないことを表現しているの?
スレーター行列式では電子を軌道に入れるすべて割り当てを考慮するので、電子を区別せず、すべて同列に扱います。そのため、$N$個の電子を入れる方法は順列の数に等しくなるので$N!$個の項が必要になります。

行列式の定義$|A|=\sum_{\sigma\in{S}}(\text{sgn}\sigma)a_{1\sigma_1}\cdots{a_{n\sigma_n}}$の$\sum_{\sigma\in{S}}$の部分(行列要素$a_{ij}$の全並び替えの和)を上手く用いています。
スレーター行列式を使うことによって、例えば軌道$\chi_1$に電子$1$が入る$\chi_1(x_1)$だけでなく、電子$2$が入る$\chi_1(x_2)$、電子$3$が入る$\chi_1(x_3)$、、という風に電子がそれぞれの軌道に入る方法がすべて対等に出てきます。
問題点:電子を入れ替えたときに電子状態の符号が変わらない
次の問題点はハートリー積では電子がフェルミ粒子であることと矛盾する点です。フェルミ粒子では2つの電子を入れ替えたときに電子状態の符号が変わる必要があります。つまり、$\Phi(x_1,x_2)=-\Phi(x_2,x_1)$である必要があります。これは全波動関数の反対称性と呼ばれています。

電子を入れ替えて符号が変わるってどういうこと?

全波動関数の反対称性はパウリの排他原理(同一空間軌道に電子は$2$個までしか入れない)の言い換えと考えてください。
ハートリー積$\Psi=\chi_1(x_1){\cdots}\chi_N(x_N)$では、$\Phi(x_1,x_2)=\Phi(x_2,x_1)$となってしまい、全波動関数の反対称性を満たすことができていません。また、その結果、パウリの排他原理も満たすことができません。
一方、スレーター行列式では、行列式を利用しているので粒子の入れ替え操作は行の入れ替え操作になります。行列式は行の入れ替えで符号を変えるので、フェルミ粒子の性質を表すことができています。

行列式の定義$|A|=\sum_{\sigma\in{S}}(\text{sgn}\sigma)a_{1\sigma_1}\cdots{a_{n\sigma_n}}$の$\text{sgn}\sigma$の部分(並び替えの偶奇置換で$\pm{1}$が変化)を上手く用いています。

$\begin{vmatrix}1&0\\0&1\end{vmatrix}=1$と$\begin{vmatrix}0&1\\1&0\end{vmatrix}=-1$だから確かに行列の行を入れ替えると行列式の符号は変わるね
スレーター行列式を使ったときのエネルギー計算

メタンでも$3628800$項が必要だから、量子化学計算なんてできる気しないよ。

安心してください。(プログラミング等に用いる)最終的な表式ではそんな大量の足し合わせは必要ありません。
スレーター行列式は大量の項($N!$個)の足し合わせで電子状態を表現しますが、実は量子化学計算(例えば電子状態のエネルギー計算)を行う上では大量の項の足し合わせは不要です。
例として$2$電子系の電子状態の運動エネルギー$T$を求めてみましょう。2電子が軌道$\chi_1$と$\chi_2$に入るときの電子状態$\Phi$はスレーター行列式を用いると$\Phi=\frac{1}{\sqrt{2}}(\chi_1(x_1)\chi_2(x_2)-\chi_1(x_2)\chi_2(x_1))$と$2!$項で表されます。
電子$1$の運動エネルギー演算子は$-\frac{1}{2}(\frac{\partial^2}{\partial{x_1}^2}+\frac{\partial^2}{\partial{y_1}^2}+\frac{\partial^2}{\partial{z_1}^2})$ですが、これを$h_1$とすると、電子$1$の運動エネルギー$T_1$は$T_1=\int{\Psi}h_1\Psi$で計算できます。

運動エネルギーの演算子の係数は$-\frac{\hbar^2}{2m}$じゃなかったっけ?

プログラムなどでは桁落ちを防ぐためにも$\hbar=1$、$m=1$などとした単位系をよく使います。
$\Psi$を代入すると次のようになります。$T_1=\frac{1}{2}\int\chi_1(x_1)h_1\chi_1(x_1)\int\chi_2(x_2)\chi_2(x_2)$$+\frac{1}{2}\int\chi_2(x_1)h_1\chi_2(x_1)\int\chi_1(x_2)\chi_1(x_2)$$-\frac{1}{2}\int\chi_1(x_1)h_1\chi_2(x_1)\int\chi_2(x_2)\chi_1(x_2)$$-\frac{1}{2}\int\chi_2(x_1)h_1\chi_1(x_1)\int\chi_1(x_2)\chi_2(x_2)$
今の段階で$2!\times2!=4$項の足し合わせを行う必要がありますが、後半の$3$項、$4$項は軌道の直交性から$0$になります。

軌道の直交性とは$\int\chi_1\chi_2=0$ということです。
その結果、結局$T_1$は$2!\times2!=4$項ではなく、$2$項の足し合わせだけから計算できることになります。
$T_1=\frac{1}{2}(\int\chi_1(x_1)h_1\chi_1(x_1)$$+\int\chi_2(x_1)h_1\chi_2(x_1))$$=\frac{1}{2}\sum_i^2\int\chi_i(x_1)h_1\chi_i(x_1)$
$T_2$も$T_1$と同じように計算できるので、$T=T_1+T_2=\sum_i^2\int\chi_i(x_1)h_1\chi_i(x_1)$とでき、スレーター行列式の規格化因子$\frac{1}{\sqrt{N!}}$由来の分数を無事なくすことができます。

以上は$2$電子系での計算ですが、$N$電子系でも同様に、$T=\sum_i^N\int\chi_i(x_1)h_1\chi_i(x_1)$とできます。
つまり、電子状態はスレーター行列式で膨大な項の足し合わせで表現する必要がありますが、量子化学計算をする(例えばプログラムなどで)では$N$項分(電子数と同じ)だけの足し合わせをするだけで運動エネルギーを求めることができます。
一般の$N$電子系に対する1電子演算子の期待値の計算方法はこちら
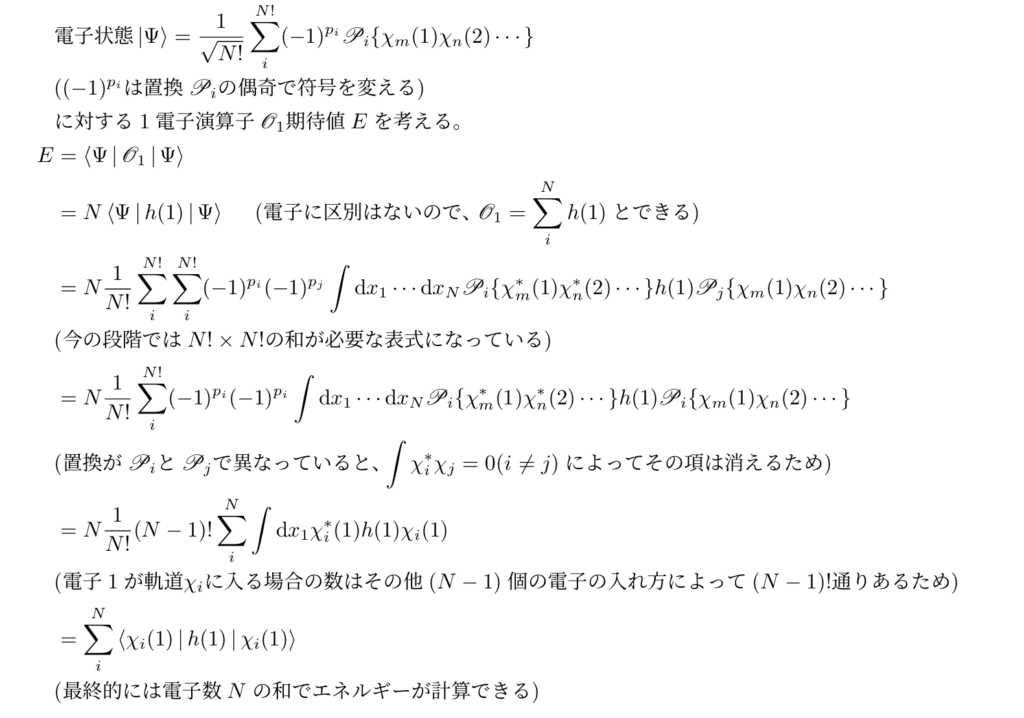

原子核からのポテンシャル$V$も同じように$V=\sum_i^N\int\chi_i(x_1)\frac{1}{r_1}\chi_i(x_1)$と$N$項の和とできるね

参考ですが、電子間反発のエネルギー$E$は$N$個の電子から$2$個を選ぶので、$N(N-1)/2$項の足し算になります。
まとめ
このページでは、量子化学計算では避けることのできないスレーター行列式について説明しました。
スレーター行列式では、行列式の定義を上手く使うことで、ハートリー積では表現できなかった電子の反区別性や全波動関数の反対称性を表せていることを紹介しました。
また、スレーター行列式では大量の項が出てきますが、実際に量子化学計算を行う上では大量の項の足し合わせは必要ないことも合わせて理解していただければと思います。