エントロピーという言葉を聞いたことがない方はほとんどいないと思いますが、具体的なイメージが湧きににくいと感じる方が多いのではないでしょうか?
熱力学を得意になるために重要になってくるのが「どれだけ具体的数値に落とし込んで熱力学を理解したか」です。
このページでは、分子動力学シミュレーション(MD)を活用し、具体的な数値を扱いながらエントロピー$S$が状態量であることを解説していきます。
状態量とは
熱力学の状態量とは系の状態だけで値が決まるもので、「どのようにしてその状態に至ったか」は値に影響を及ぼしません。例えば、内部エネルギー$U$や温度$T$などは状態量です。

「どのようにしてその状態に至ったか」ってどういうこと?

例えば、電熱線で冷水をあっためて$50℃$温水を作ったのか、沸騰水が冷えて$50℃$温水ができたのか、といった経緯のことだよ。
熱力学において状態量であるという情報は非常に重要です。例えば、熱機関の効率$\eta$を計算する際、「熱サイクルを1周した際の内部エネルギー変化量$\Delta{U}=0$である」という事実を使いますが、これは内部エネルギー$U$が状態量であることを利用しています。

一方で、熱力学の第一、第二法則で状態量$U$や$S$とかかわりがありますが、熱量$Q$や仕事量$W$は状態量ではありません。
エントロピーも状態量?
結論からいうと、エントロピー$S$も内部エネルギー$U$と同じく状態量です。ですが、エントロピー$S$については状態量であることのイメージが湧きにくい方も多いのではないでしょうか?

エントロピー$S$は熱$Q$と結びつきが強いし、温度みたいに直接測定もできないから、状態量といわれてもピンとこないよ。

それではMDの結果を利用してエントロピー$S$が状態量であることを具体的に調べてみましょう。
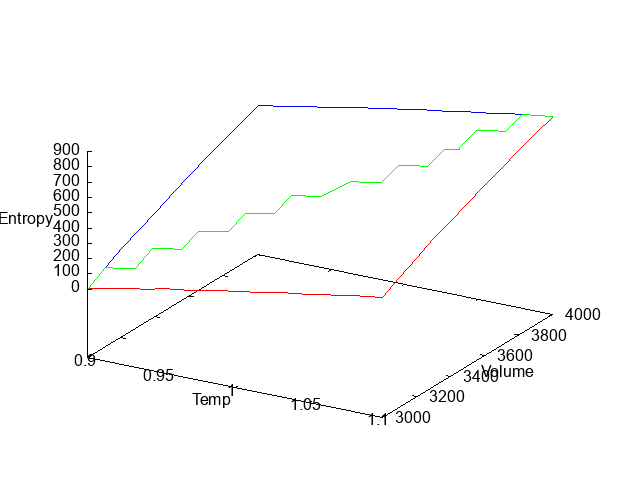
エントロピー変化量を計算
温度$T$が$0.9$~$1.1$の間、体積$V$が$3000$~$4000$の間の様々な条件でMDを行いましたので、その結果をもとにエントロピーが状態量であることを確認していきましょう。

MDはポテンシャルエネルギー$V(r)=(1/r)^{12}-(1/r)^6$に則って動く単原子状分子を対象に行いました。
分子動力学シミュレーションの結果をcsvファイルでおいておきます。
では、エントロピーを求める熱力学積分について、下の3種類の経路がエントロピー$S$の計算結果に影響しないことを確認していきましょう。

経路①~③は同じ状態からスタートし、同じ状態へ至りますが、そこに至る経路が全く異なります。
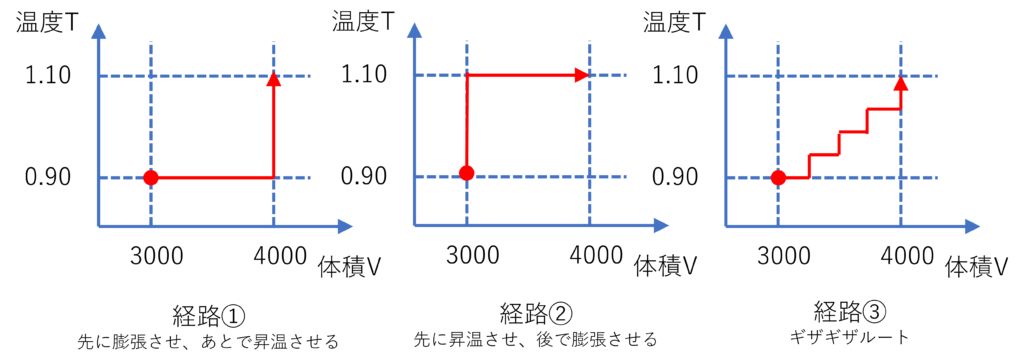

経路①は膨張→昇温ルート、経路②は昇温→膨張ルート、そして経路③はギザギザルートだね。
経路①
まずは、経路①として、体積$3000$から$4000$へ圧縮させた後、温度を$0.9$から$1.1$へ昇温させたときのエントロピー変化を計算してみましょう。
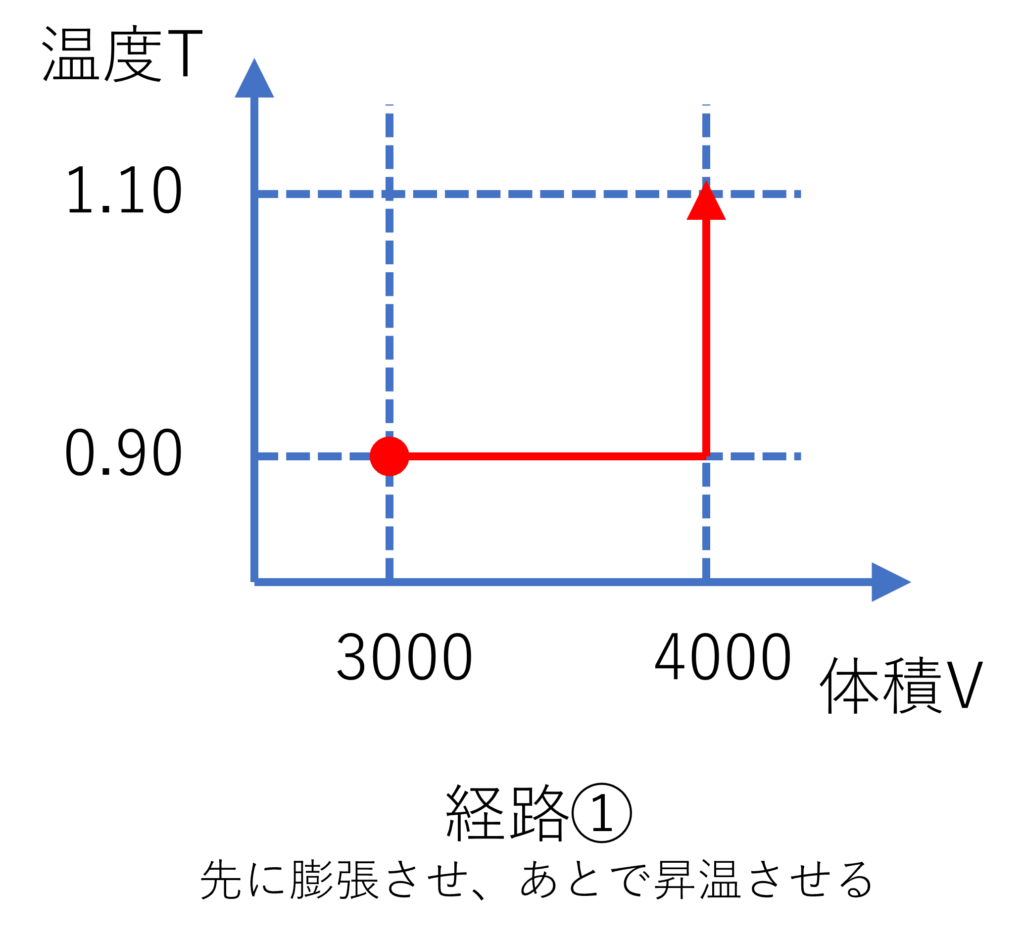

そういえばエントロピー$S$ってどうやって計算できるの?
試しに温度$T=0.90$で体積$V=3000$から$3100$まで等温膨張させた場合のエントロピー変化$\Delta{S}$を計算してみましょう。
| 温度$T$ | $0.90$ | |||
| 体積$V$ | $3000$ | 等温膨張→ | $3100$ | $dV=$$100$ |
| 内部エネルギー$U$ | $976.4$ | $988.6$ | $dU=$$12.2$ | |
| 圧力$P$ | $0.478$ | $0.454$ | $\bar{P}=$$0.466$ | |
使うのは熱力学第一法則$dS=\frac{dU}{T}+\frac{P}{T}dV$です。注意点として、圧力$P$は平均値$\bar{P}=\frac{0.478+0.454}{2}=0.466$を利用しましょう。これらから$dV=100$だけ等温膨張した後のエントロピー変化量は$dS=12.2/0.9+0.466/0.9\times100=65.3$となります。

この手続きをひたすら繰り返しすことで$(T,V)=(0.9,3000)$から$(T,V)=(0.9,4000)$での$\Delta{S}$を求めることができます。
さて、計算結果は↓の図です。膨張が終わったところでエントロピー$S$は$526.9$まで上昇します。さらに、温度が昇温し終わったところで最終的に$848.6$となります。
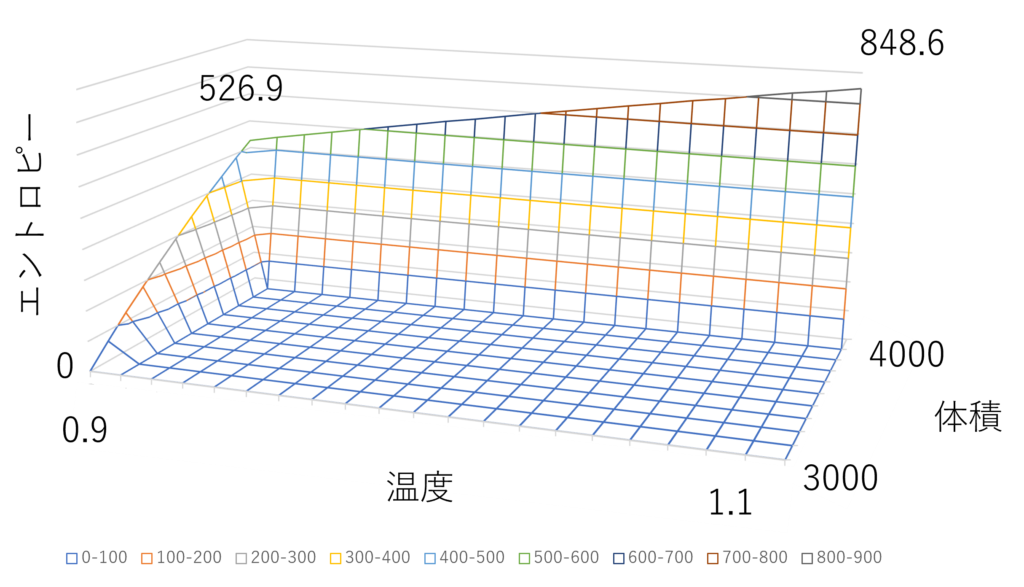

等温膨張は$dS=\frac{dU}{T}+\frac{P}{T}dV$で、等積昇温は$dS=\frac{dU}{T}$でエントロピー変化$\Delta{S}$が計算できるんだね。
経路②
次に、経路②として、温度を$0.9$から$1.1$へ昇温させた後、体積を$3000$から$4000$へ膨張させるときのエントロピー変化を計算してました。
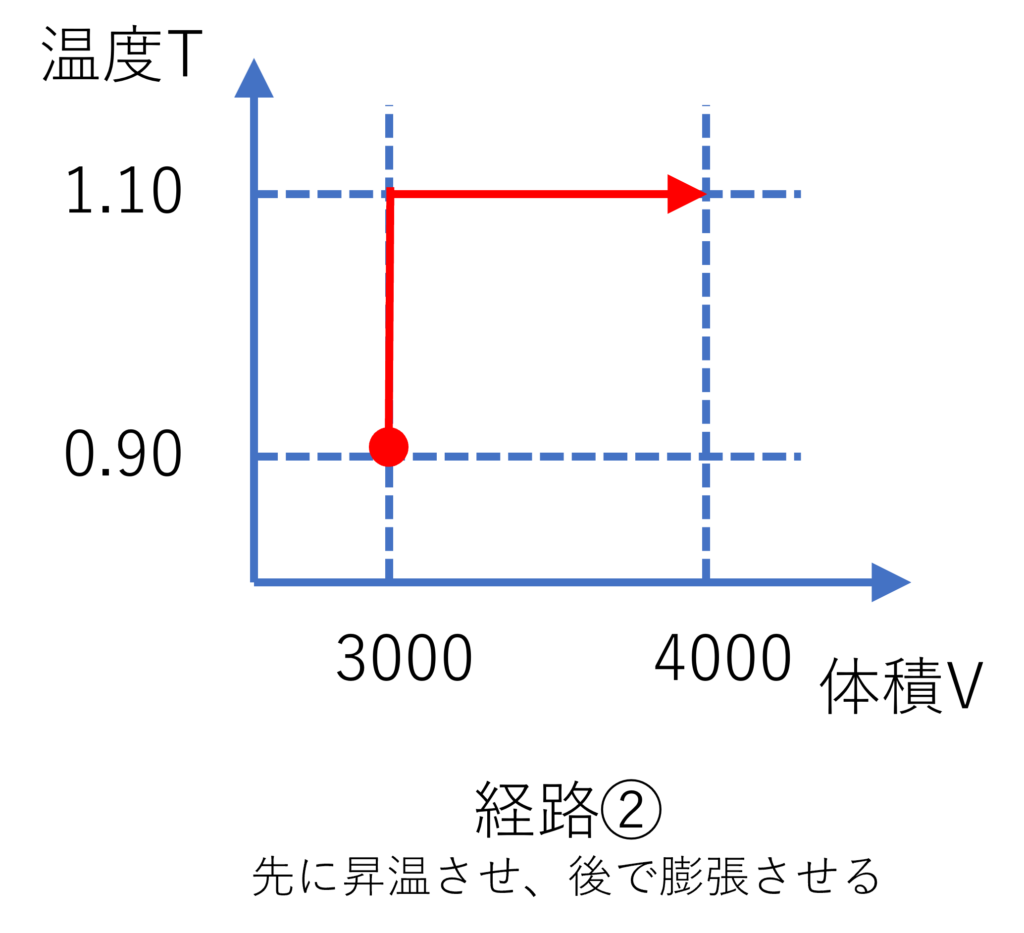

計算方法は「経路①」の時と全く同じです。

等温膨張は$dS=\frac{dU}{T}+\frac{P}{T}dV$で、等積昇温は$dS=\frac{dU}{T}$を利用だね!最終的なエントロピーは$841.3$だったよ!
まとめ
さらに、「ギザギザルート」である、経路③の場合も計算すると、温度$T=1.1$、体積$V=4000$ではエントロピー$S=845.4$となり、やはり経路1や経路2とほとんど差がないことがわかります。
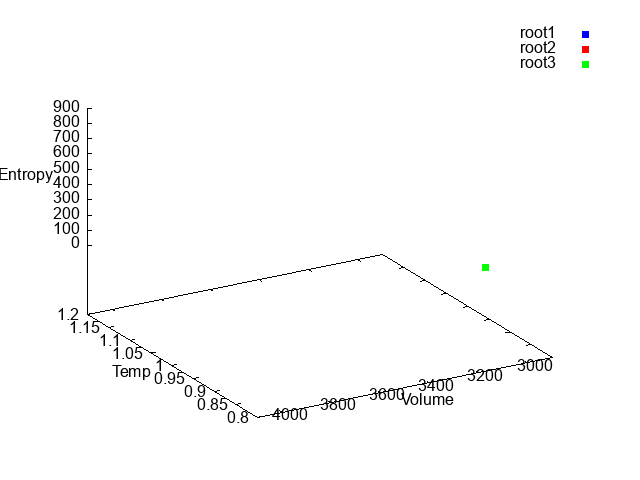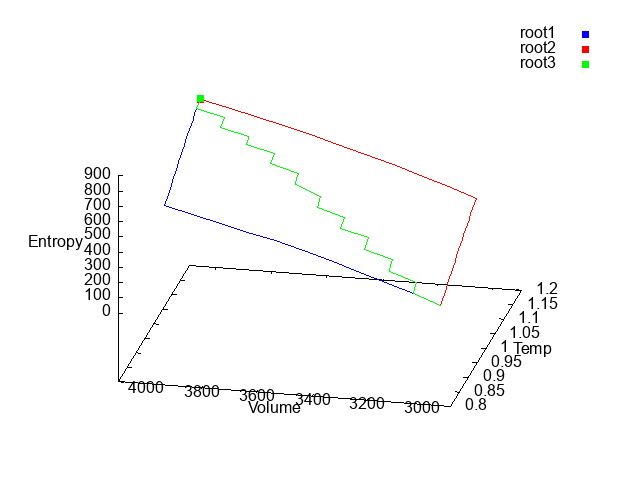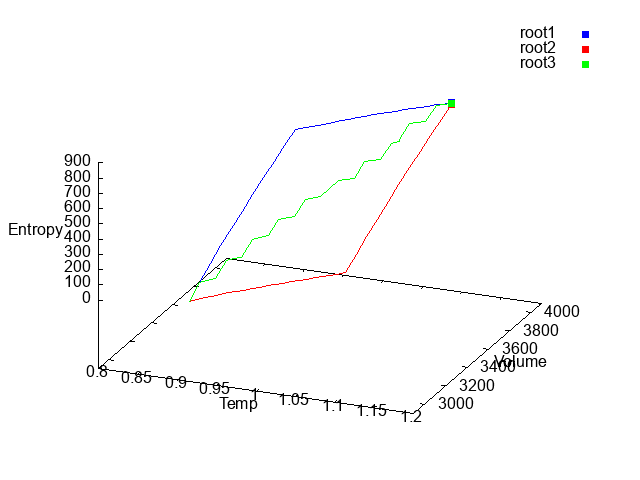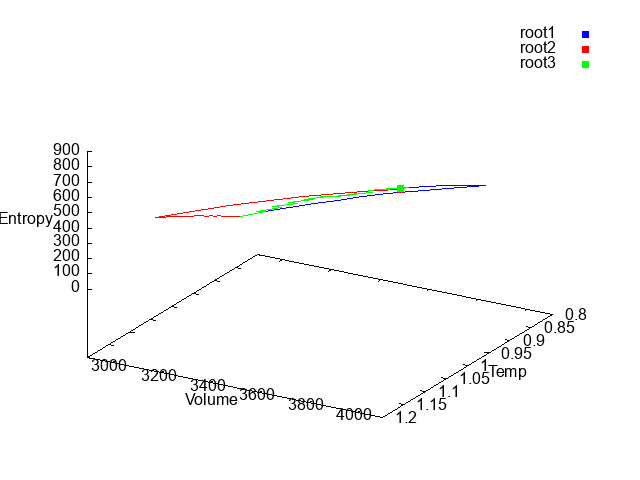
経路1と経路2、経路3で求めたエントロピー変化量$\Delta{S}$をまとめると↓表のようになります。誤差は$1\%$未満でした。
| エントロピー変化量$\Delta{S}$ | 誤差 | |
| 経路1 | $848.6$ | —— |
| 経路2 | $841.3$ | $0.8\%$ |
| 経路3 | $845.4$ | $0.3\%$ |

かなりの精度でエントロピー変化量が経路によらないことを確認できたのではないでしょうか。
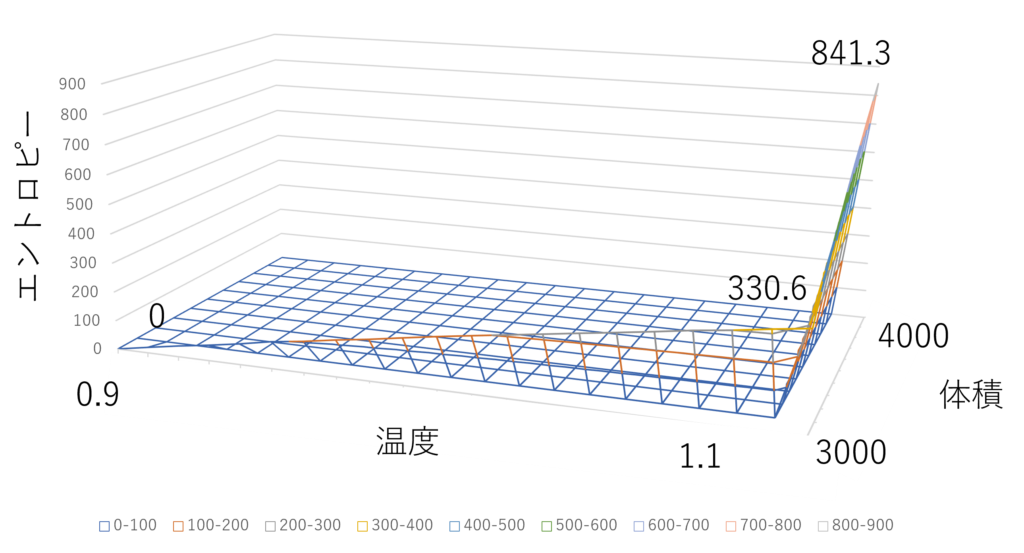
3つのルートをまとめて表示すると↓の図のようになります。青が経路①、赤が経路②、緑が経路③になりますが、いずれもほぼ同じ点に収れんしていることがわかります。


エントロピー$S$が熱力学変化の過程によらず最終的な熱力学的状態で値が決まることを確認できたかと思います。









