MDでは通常の運動方程式($ma=F$)に従うだけでは、温度一定のシミュレーションはできません。
このページではMDでよく用いられる能勢・フーバー法(NVT一定)のアルゴリズムを確認し、実際に単原子分子に対して分子動力学シミュレーションを行った結果をご紹介します。
- NVTが一定となる各粒子の運動方程式
- NVTが一定の分子動力学シミュレーションアルゴリズム(能勢・フーバーのアルゴリズム)
- NVTが一定のシミュレーション結果
NVT一定のシミュレーション
化学では断熱材で覆われた環境(NVE一定)よりも、オイルバスなどで周辺温度を一定にした実験(NVT一定)のほうが圧倒的に多いです。

つまり、NVTが一定のシミュレーションのほうがNVEよりも実際の実験に近いもののシミュレーションにつながります。
このNVTが一定の分子動力学シミュレーション(MD)を実現できるのが「能勢・フーバーの方法」です。結論を述べると、NVEが一定の速度ベルレ法に3つほど式を加えることでNVTが一定のMDを行うことができます。
能勢・フーバーの運動方程式
能勢・フーバーの運動方程式は↓のように書くことができることが知られています。
$\frac{\text{d}r_i}{\text{d}t}=\frac{p_i}{m_i}$
$\frac{\text{d}p_i}{\text{d}t}=F_i-\zeta{p_i}$
$\frac{\text{d}\zeta}{\text{d}t}=\frac{3N}{Q}(T-T_{\text{set}})$
$T=\frac{1}{2}\sum_i\frac{p_i^2}{m_i}$
この運動方程式を解けば温度を$T_{\text{set}}$に制御しつつMDを行うことができます。

$Q$とか$\zeta$とか見慣れない変数が増えたけどこれはなに?

$Q$と$\zeta$について順番に解説しますね。
$Q$は熱浴の質量を表すパラメーターです。例えば$Q=5.0$などと決めてシミュレーションを行い、シミュレーション途中で値は変化しません。
$\zeta$は系の運動量を制御する機能を持ちます。例えば系の温度$T$が設定温度$T_{\text{set}}$よりも大きくなった場合、$\frac{\text{d}\zeta}{\text{d}t}=\frac{3N}{Q}(T-T_{\text{set}})$によって$\zeta$は大きくなり、$\frac{\text{d}p_i}{\text{d}t}=F_i-\zeta{p_i}$を通して粒子の速度(温度)を下げます。初期値は$0$などとしてMDを始めます。

熱浴の質量というと$Q$は大きいほうがいいの?

そうでもありません。$Q$は大きすぎると温度制御が大きく振動してしまうこともあるため、注意が必要です。
また、この運動方程式における保存量は運動エネルギー+ポテンシャルエネルギーではなく、温浴の効果を足したものが保存量$H$になります。$H=\sum\frac{p_i^2}{2m_i}+\sum{V}(r_{ij})+\frac{\zeta^2{Q}}{2}+3NT_{\text{set}}\eta$です。

運動方程式にはない変数$\eta$が突然出てきたよ?

この$\eta$は$\zeta$のみから計算でき、$\frac{\text{d}\eta}{\text{d}t}=\zeta$で時間発展します。ほかの変数には影響を与えません。
能勢・フーバー法のアルゴリズム
NVTが一定となる能勢・フーバーの方法についてもNVEのアルゴリズムを少し拡張するだけで実現できてしまいます。下の①、④、⑥がNVE一定のアルゴリズムから増えた手続きですが、そこまで難しくはありません。
- $p_i(t+\frac{\Delta{t}}{2})=p_i(t)*\exp(-\zeta*\frac{\Delta{t}}{2})$
- $p_i(t+\frac{\Delta{t}}{2})=p_i(t+\frac{\Delta{t}}{2})+F_i*\frac{\Delta{t}}{2}$
- $x_i(t+\Delta{t})=x_i(t)+\frac{p_i(t+\frac{\Delta{t}}{2})}{m_i}*\Delta{t}$
- $\zeta(t+\Delta{t})=\zeta(t)+(\sum\frac{p_i^2}{m_i}-3NT_{\text{set}})\frac{\Delta{t}}{Q}$
- $p_i(t+\Delta{t})=p_i(t+\frac{\Delta{t}}{2})+F_i*\frac{\Delta{t}}{2}$
- $p_i(t+\Delta{t})=p_i(t)*\exp(-\zeta*\frac{\Delta{t}}{2})$
この①~⑥を繰り返すことでNVTが一定の分子動力学シミュレーションを行うことができます。
単純なNVEよりもステップは増えるものの、収束計算などの複雑な手続きなしでNVTが一定の能勢・フーバーのアルゴリズムを実装できます。

このアルゴリズムで精度よく計算できる理由は解析力学の知識や鈴木・トロッター展開などを用いると見通しよく導出することができます。
実際のシミュレーション結果(NVT一定)
実際に能勢・フーバーのアルゴリズムをプログラミングし、1000粒子系に対して目標温度$T_{\text{set}}=1.0$としてシミュレーションを実施しました。時間のステップ幅は$\Delta{t}=0.005$としています。

$Q$の大きさによる違いを調べるため、$Q=10$と$Q=100$の2通りでMDを実施してみました。
温度$T$の制御結果について
最も興味のある温度$T$の制御結果は↓の図です。温度$T=1.0$の周辺で温度が振動しています。
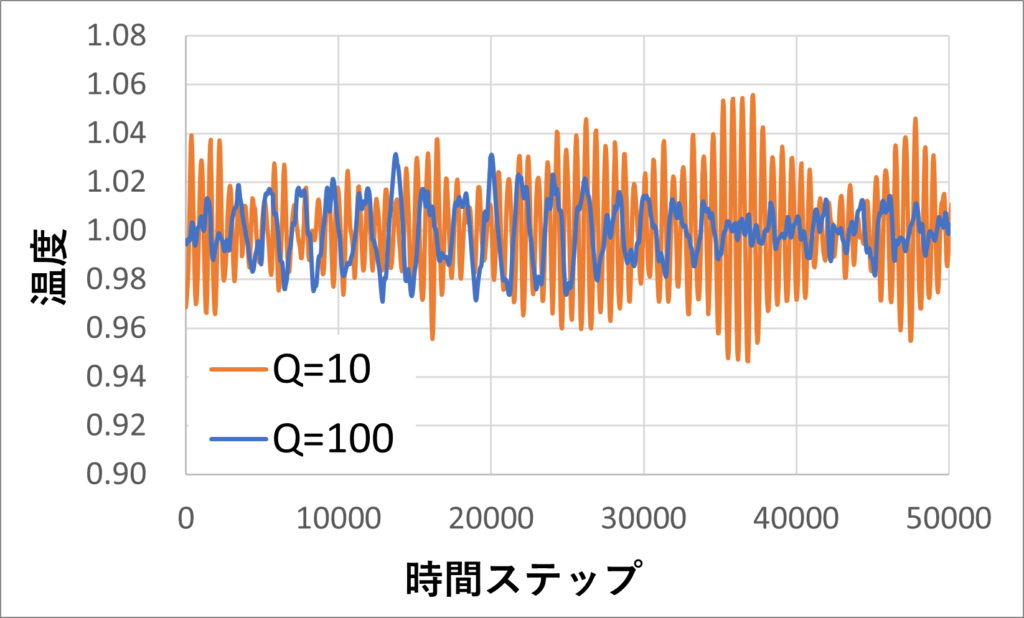

NVT一定のシミュレーションといっても、$T=1.0$がずっと続くわけではないんだね。

変数$\zeta$が現状温度$T$と目標温度$T_{\text{set}}$の差によって大きくなったり、小さくなったりして温度を制御するからです。
内部エネルギー$E$について
NVEが一定のシミュレーションでは内部エネルギーは$0.005$程度の範囲で振れ幅を持っていましたが、NVTが一定の場合、もちろん内部エネルギー$E$は一定にはなりません。
$Q=10$の場合も$Q=100$の場合も平均値はほぼ同じですが、どちらもある程度($50$程度)の振れ幅を持って揺らいでいます。
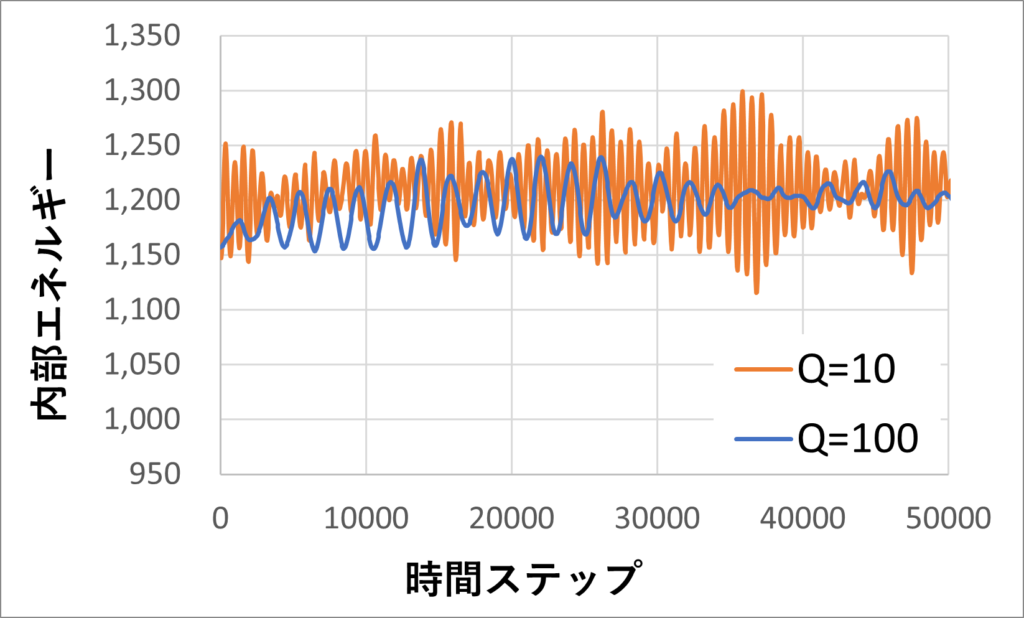

温度$T$を一定としているため、内部エネルギー$E$が一定であることは犠牲になっているんだね。。
能勢・フーバー法で一定になるものは?
NVTでは温度$T$も内部エネルギー$E$も厳密には一定にはなりませんでした。では何が一定になるのでしょうか。
能勢・フーバー法では温浴の効果を足したエネルギー$H$が保存されます。次の表式です。$H=\sum\frac{p_i^2}{2m_i}+\sum{V}(r_{ij})+\frac{\zeta^2{Q}}{2}+3NT_{\text{set}}\eta$です。
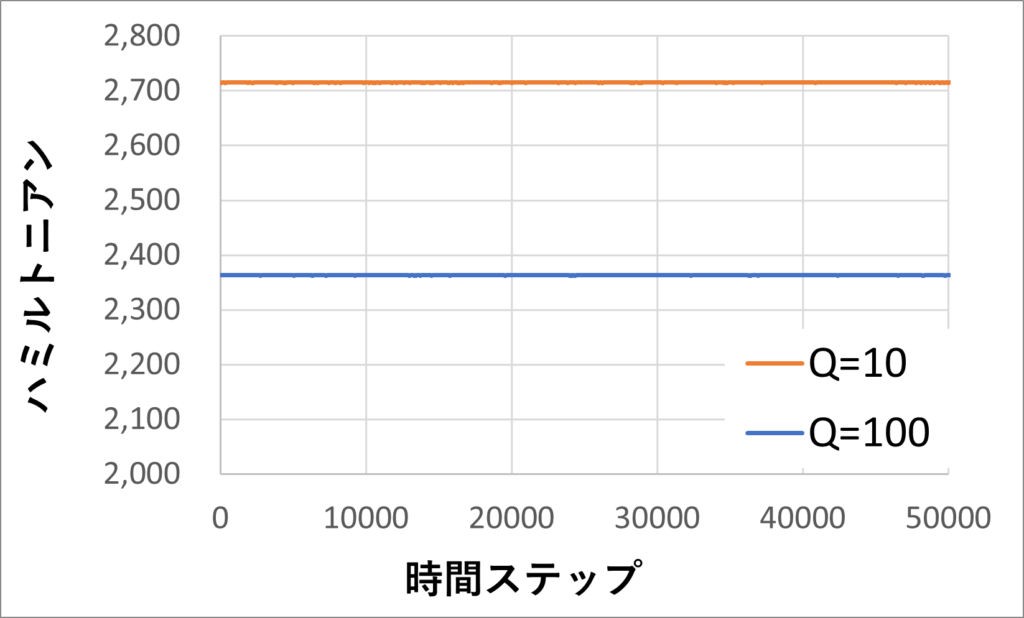

熱浴の質量$Q$の大きさによって保存量$H$の大きさは違うけど、どちらも一定の数値を維持しているね。
まとめ
このページでは次のことを確認しました。
- NVTが一定となる各粒子の運動方程式
- NVTが一定の分子動力学シミュレーションアルゴリズム
- NVTが一定のシミュレーション結果
能勢・フーバーの温度制御について、方程式とアルゴリズム、そしてシミュレーション結果まで見てきました。アルゴリズムはかなりシンプルですが、狙いの温度に制御できる強力な方法であることを理解していただければと思います。
NVT一定の分子動力学シミュレーションは分子動力学シミュレーションのなかでもかなり基本的でよくつかわれる手法なので、みなさんも一度試してみてください。











