熱力学第二法則であるエントロピー増大の法則はとても有名です。
このエントロピー増大の法則は「低温から高温に熱は移動しない」という当たり前の経験(クラウジウスの法則)から4ステップ程度で簡単に導くことができます。
このページではクラウジウスの法則を用いて、エントロピー増大の法則までを順序だてて導いていきます。

ステップ1:トムソンの法則
まずは、クラウジウスの法則(低温から高温に熱は移動しない)からトムソンの法則(熱源から得た熱の全てを仕事には変えられない)を導きましょう。
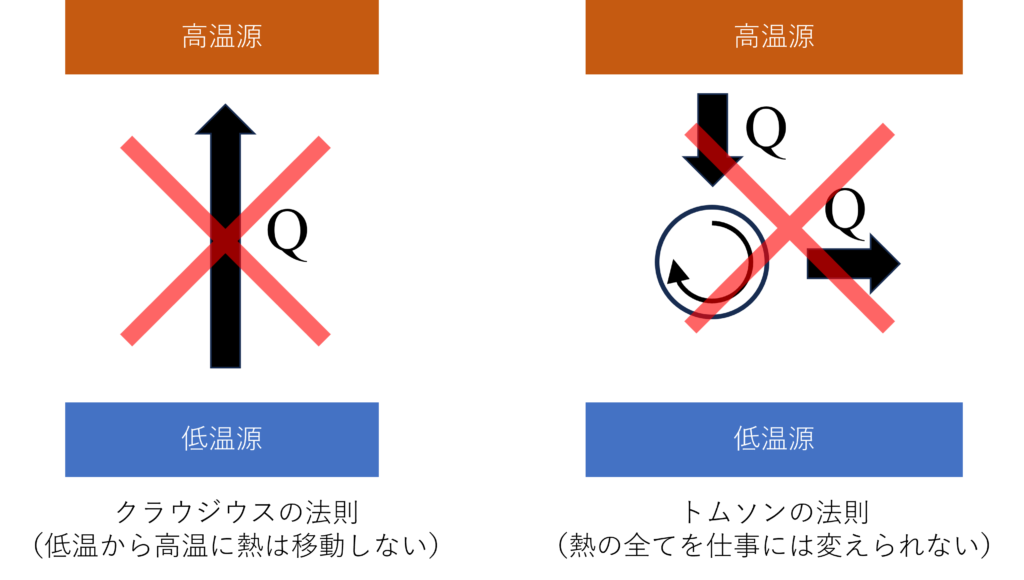
もし、トムソンの法則に反したプロセス(熱$Q$の全てを仕事$W$に変えられる)があるとします。すると、この仕事$W$を使って熱ポンプを稼働させると、プロセス全体では低温源から高温源に熱が一人でに移動していることになり、クラウジウスの法則に反するプロセスがあることになります。
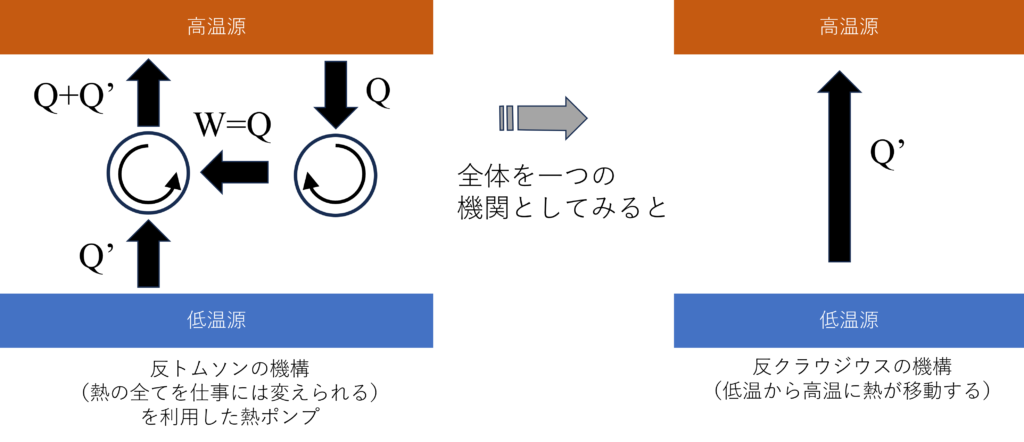
これは$\overline{トムソン}$⇒$\overline{クラウジウス}$が正しいこと示しているので、対偶をとることでクラウジウスの法則⇒トムソンの法則が示されます。

ステップ2:カルノーの定理
次に、トムソンの法則からカルノーの定理(二つの熱源を利用する可逆機関の効率は全て等しく、不可逆機関より高い。可逆機関の効率は熱源の温度だけで決まる。)を導きましょう
可逆機関の効率は全て等しい
まず、「二つの熱源を利用する可逆機関の効率は全て等しく、不可逆機関より高い。可逆機関の効率は熱源の温度だけで決まる。」の 部分を示します。
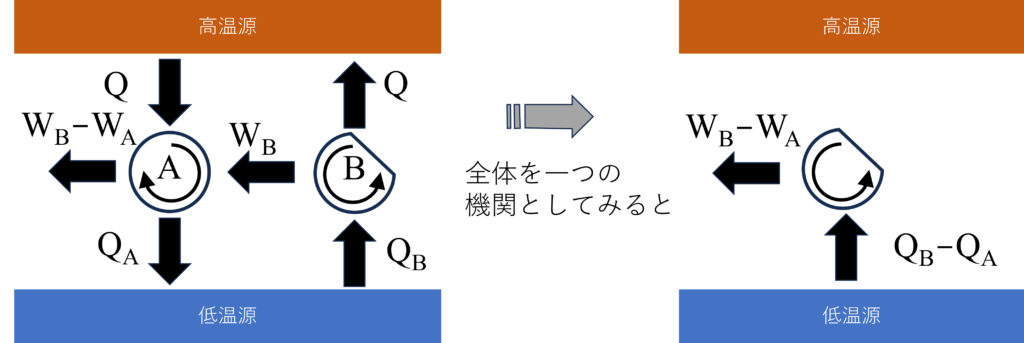
図のような可逆サイクル$A$と$B$を考えましょう。高温源からはサイクル$A$、$B$ともに同じ$Q$の熱を抜き取りますが、低温源にはそれぞれ$Q_A$、$Q_B$の熱を排出するとします。
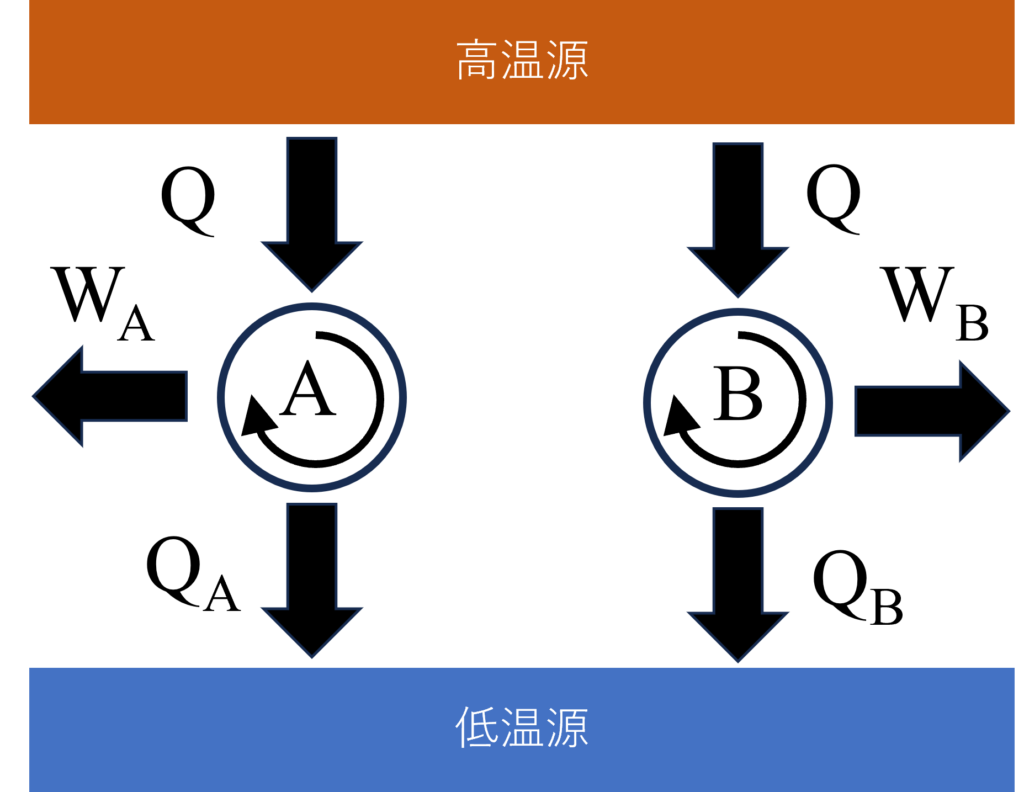

熱力学第一法則からサイクル$A$と$B$が成す仕事は$W_A=Q-Q_A$、$W_B=Q-Q_B$だね。
もし、$W_A\gt{W_B}(Q_A\lt{Q_B})$であったとすると、$W_A$の一部を利用して可逆サイクル$B$を逆運転することで、1つの熱源から熱を受け取って、すべてを仕事にできることになりますが、これはトムソンの法則に反します。したがって、$W_A\le{W_B}(Q_A\ge{Q_B})$が必要です。
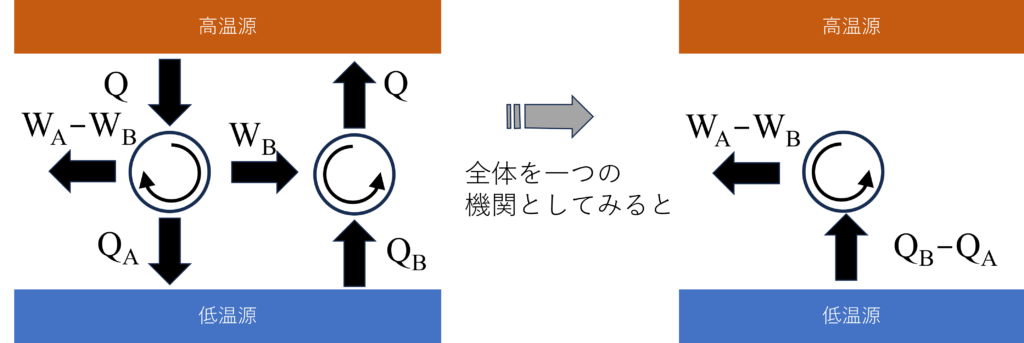
同じ考えで、$W_A\lt{W_B}$と仮定した場合もトムソンの法則に反するので、結果$W_A={W_B}$でなければならないことになります。つまり、可逆機関$A$と$B$の効率$\eta_A=\frac{W_A}{Q}$と$\eta_B=\frac{W_B}{Q}$は同じ値になります。
ここまでで、カルノーの定理のうち、「二つの熱源を利用する可逆機関の効率は全て等しい。」が言えています。
なお、高熱源、低温源との熱のやり取り$Q_H$、$Q_L$を用いると、可逆機関の熱効率は$\eta=\frac{W}{Q_H}=1-\frac{Q_L}{Q_H}$と熱量比だけで決まります(作業流体や機構は影響しない)。
不可逆機関だった場合
次に、「二つの熱源を利用する可逆機関の効率は全て等しく、不可逆機関より高い。可逆機関の効率は熱源の温度だけで決まる。」の 部分を示します。
そのために、サイクル$B$を不可逆サイクルとしましょう。
$W_A\lt{W_B}$とすると、先ほどの議論と同じように、一つの熱源から熱を受け取って、それを全て仕事にできることになるので、トムソンの法則に反します。
また、$W_A={W_B}$の場合は、可逆サイクル$A$を逆回転させることで、不可逆サイクル$B$による変化(熱移動、仕事量)をすべて打ち消してもとに戻せます。これはサイクル$B$が可逆サイクルであることになるので矛盾します。
以上から、$W_A\gt{W_B}$だけが許されるので、可逆サイクルの熱効率$\eta_A=\frac{W_A}{Q}$は不可逆サイクルの熱効率$\eta_B=\frac{W_B}{Q}$よりも優れます。

サイクル$A$を逆転させると、全体では外部から仕事を受けとり、それを熱として捨てることになるね。

仕事を熱にすることは、摩擦等でありふれています(トムソンの法則に反しない)。
したがって、カルノーの定理のうち、「二つの熱源を利用する可逆機関の効率は全て等しく、不可逆機関より高い。」が言えます。
熱力学温度の導入
最後に、「二つの熱源を利用する可逆機関の効率は全て等しく、不可逆機関より高い。可逆機関の効率は熱源の温度だけで決まる。」の 部分を示します。
「可逆機関の効率は熱源温度で決まる」を明らかにするため、可逆機関の効率は全て等しいという性質から、$\frac{Q_L}{Q_H}=\frac{\theta_L}{\theta_H}$とする熱力学的温度$\theta$を導入しましょう。
熱力学温度$\theta$として状態方程式$PV=nRT$に従う理想気体温度$T$を用いると、可逆機関の効率は2つの熱源温度を利用して$\eta=1-\frac{T_L}{T_H}$とできます。

$\theta$の1目盛の大きさを理想気体温度$T$と同じにすると、$\theta=T$になります。
以上から、トムソンの原理⇒カルノーの定理が言えます。

ステップ3:クラウジウスの関係式
カルノーの定理から、熱源が2つだけの可逆サイクルの場合、熱効率$\eta$は熱源の温度だけで決まります($\eta=1+\frac{Q_2}{Q_1}=1-\frac{T_2}{T_1}$)。つまり、$\frac{Q_1}{T_1}+\frac{Q_2}{T_2}=0$です。
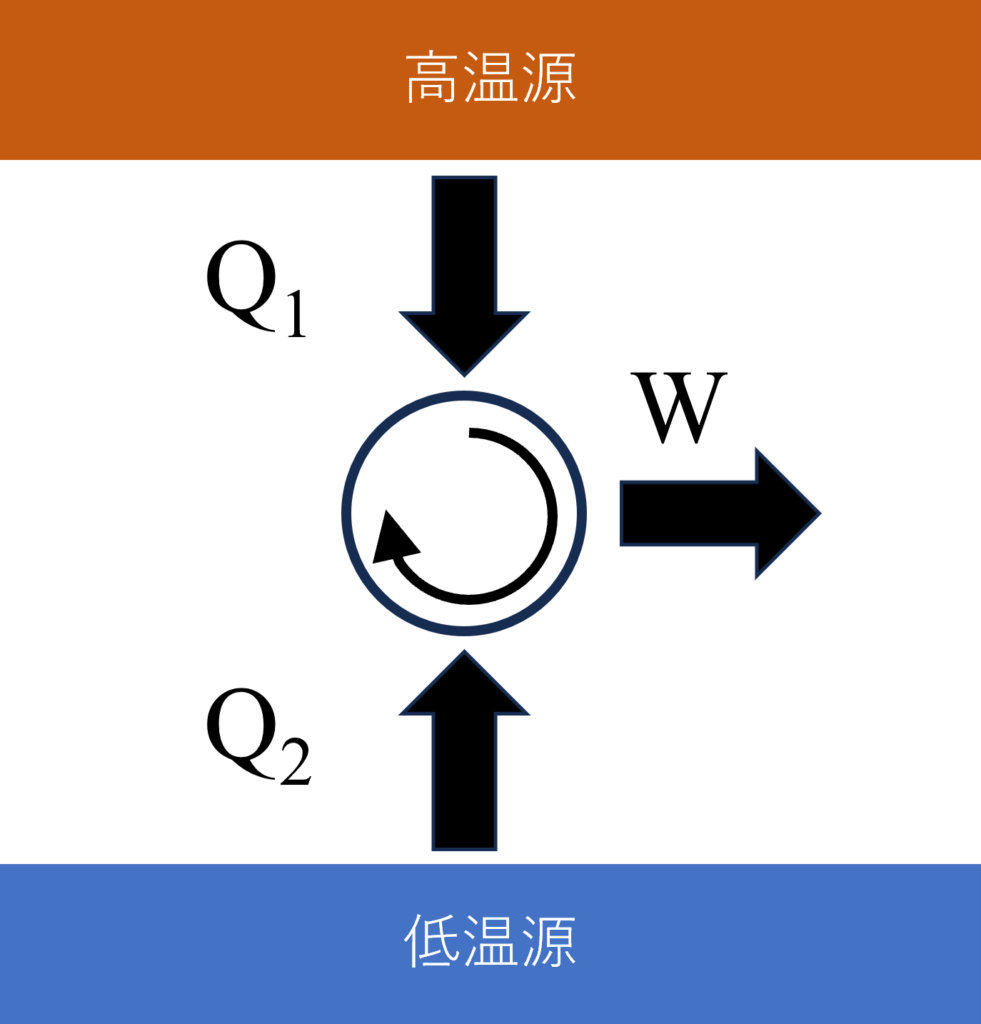

低温への熱排出量$Q_L$を低温からの熱供給量$Q_2=-Q_L$と捉えている点に注意です。
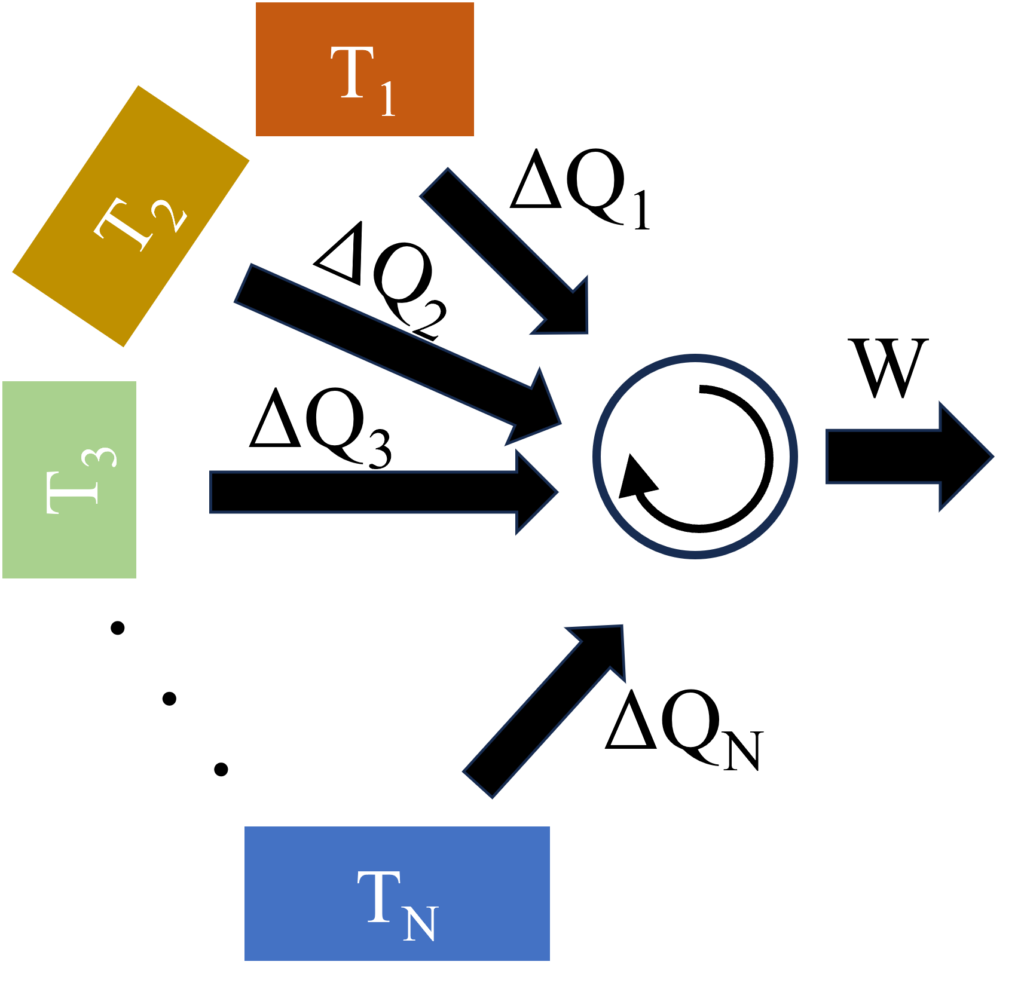
熱源を$N$個に拡張し、やり取り熱量を微小化して$\Delta{Q}_i$とすると、$\sum_i^N\frac{\Delta{Q_i}}{T_i}=\frac{\Delta{Q_1}}{T_1}+\frac{\Delta{Q_2}}{T_2}+\cdots=0$です。$\sum$部分を$\oint$に置き換えると、$\oint\frac{\text{d}Q}{T}=0$になります。
状態$1$と$2$を通る可逆サイクルへ適用させると$\oint\frac{\text{d}Q}{T}=\int^{1\to{a}}_{\to2}\frac{\text{d}Q}{T}+\int^{2\to{b}}_{\to1}\frac{\text{d}Q}{T}=0$です。

第2項の経路を逆にすると、$\int^{1\to{a}}_{\to2}\frac{\text{d}Q}{T}=\int^{1\to{b}}_{\to2}\frac{\text{d}Q}{T}$となります。これはエントロピー変化量を$\text{d}S=\frac{\text{d}Q}{T}$とすると、$\int_{可逆}\frac{\text{d}Q}{T}$は積分経路に依らないことからエントロピー$S$は状態量であることを表しています。
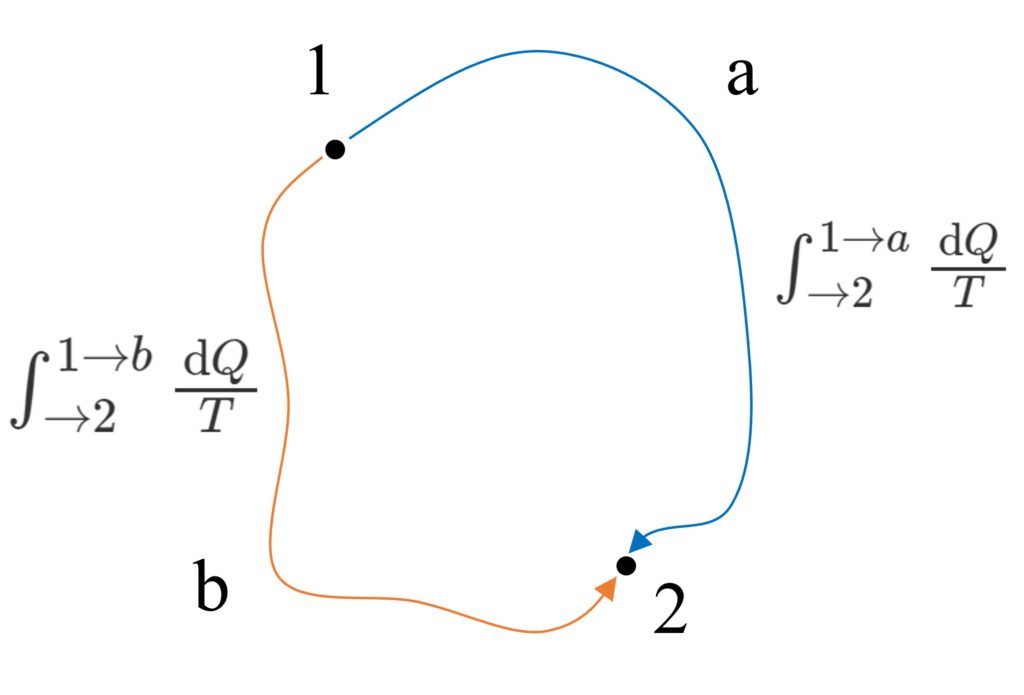

この論証と結論は熱力学第二法則で最も重要です

もし、温度$T_j$と$T_{j+1}$で動作する可逆サイクルを不可逆サイクルに変えると、カルノーの定理から不可逆サイクルの効率は可逆サイクルより劣るので、$\frac{\Delta{Q}_j}{T_j}+\frac{\Delta{Q}_{j+1}}{T_{j+1}}\lt0$になります。したがって、不可逆サイクルでは$\oint\frac{\text{d}Q}{T}\lt0$(クラウジウスの不等式)になります。
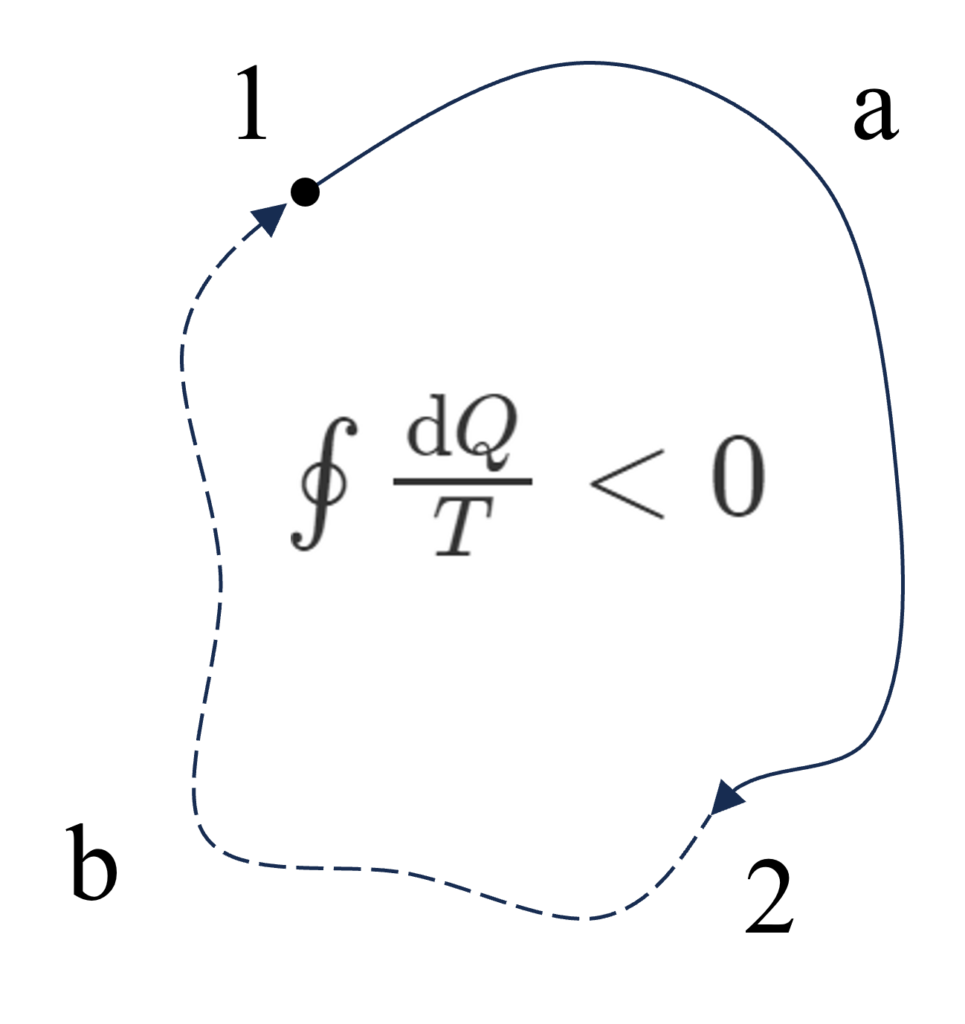
ここまでで、カルノーの定理⇒クラウジウスの不等式を導けました。

ステップ4:エントロピー増大の法則
不可逆過程を含むサイクルでは、クラウジウスの不等式から$\oint\frac{\text{d}Q}{T}\lt0$です。この経路積分を可逆部分と不可逆部分に分けましょう。$\oint\frac{\text{d}Q}{T}=\int^{1\to2}_{不可逆}\frac{\text{d}Q}{T}+\int^{2\to1}_{可逆}\frac{\text{d}Q}{T}\lt0$
$\int^{1\to2}_{可逆}\frac{\text{d}Q}{T}$はエントロピー変化量に置き換えられるので、この不等式は$\Delta{S}_{{1\to2}}\gt\int^{1\to2}_{不可逆}\frac{\text{d}Q}{T}$とできます。したがって、温度$T$の系が不可逆的に熱$\text{d}Q$を受け取り、エントロピーが$\text{d}S$変化するとき、$\text{d}S\gt\frac{\text{d}Q}{T}$が成り立ちます。
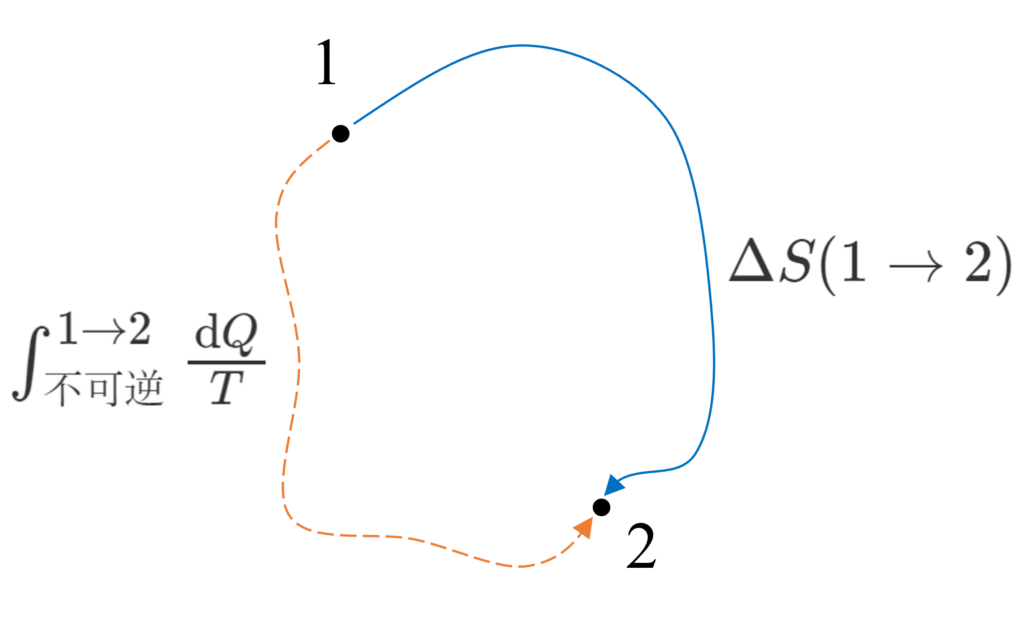
もし、系が熱を受け取らない場合($\text{d}Q=0$)は単純に$\text{d}S\gt0$となり、これはエントロピー増大の法則(孤立系、及び断熱系において不可逆変化が生じた場合、その系のエントロピーは増大する)です。
したがって、クラウジウスの不等式($\oint\frac{\text{d}Q}{T}\lt0$)からエントロピー増大の法則($\text{d}S\gt0$)を導くことができました。

まとめ
このページではクラウジウスの法則(低温から高温に熱は移動しない)という当たり前と感じられる法則からからエントロピー増大の法則を導くことができました。
このページで解説した内容は熱力学第二法則を示すうえで、よく用いられる論法(例えばクラウジウスの法則とトムソンの法則が同一内容であること)です。非常に完成されている論法ですので、一度皆さんも考えてみてください。











