熱交換器には$Q=AU\Delta{T}_{\text{LM}}$という伝熱量を計算する基本式があります。この$\Delta{T}_{\text{LM}}$が対数平均温度と呼ばれるもので、このページの主役です。
私が初めて対数平均温度を知ったとき、「また経験則か？」「相乗平均ではだめなの？」と少し斜に構えてしまっていました。（そんな過去の私に朗報ですが、）対数平均温度を使う理由には理論的な背景がしっかりとあります。
このページでは、向流熱交換器と並流熱交換器における対数平均温度差$\Delta{T}_{\text{LM}}$を具体的に計算してもらいつつ、熱交換器の基本式が$Q=UA\Delta{T}_{\text{LM}}$になる理由まで解説します。
【すぐ使える】LMTD（対数平均温度差）計算機
熱交換器では、流体間の「温度差」が大きくなればなるほど、伝熱量はもちろん大きくなります。
工場にあるような熱交換器では、この「温度差」として対数平均温度差$\Delta{T}_{\text{LM}}$を用いる必要があります。
$\Delta{T}_{\text{LM}}$を下の計算機で実際に計算してみてください
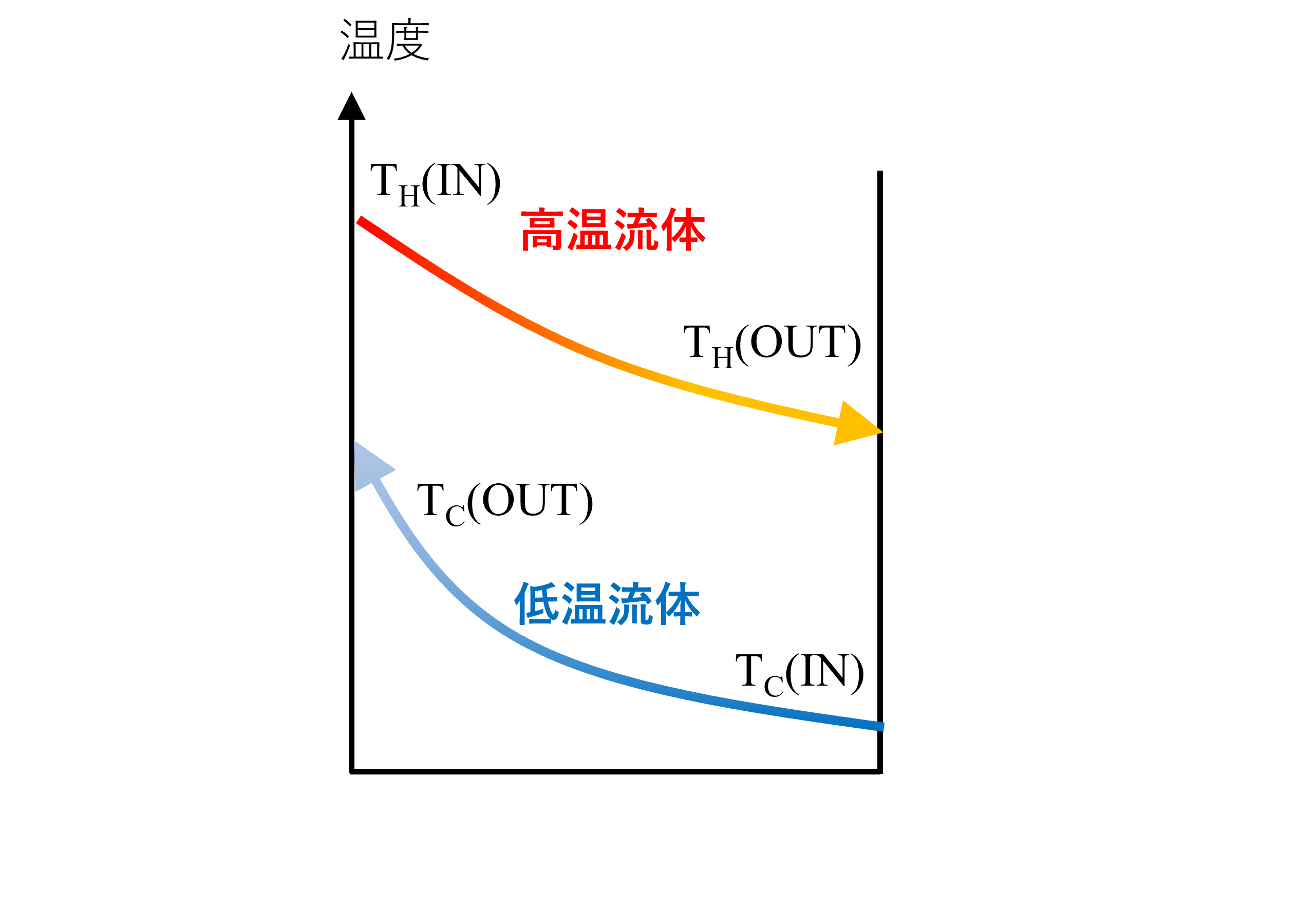
向流型熱交換器の場合
高温流体と低温流体を逆方向に流すのが「向流型熱交換器」です。向流は並流に比べて、熱交換器としての効率は高くなります。
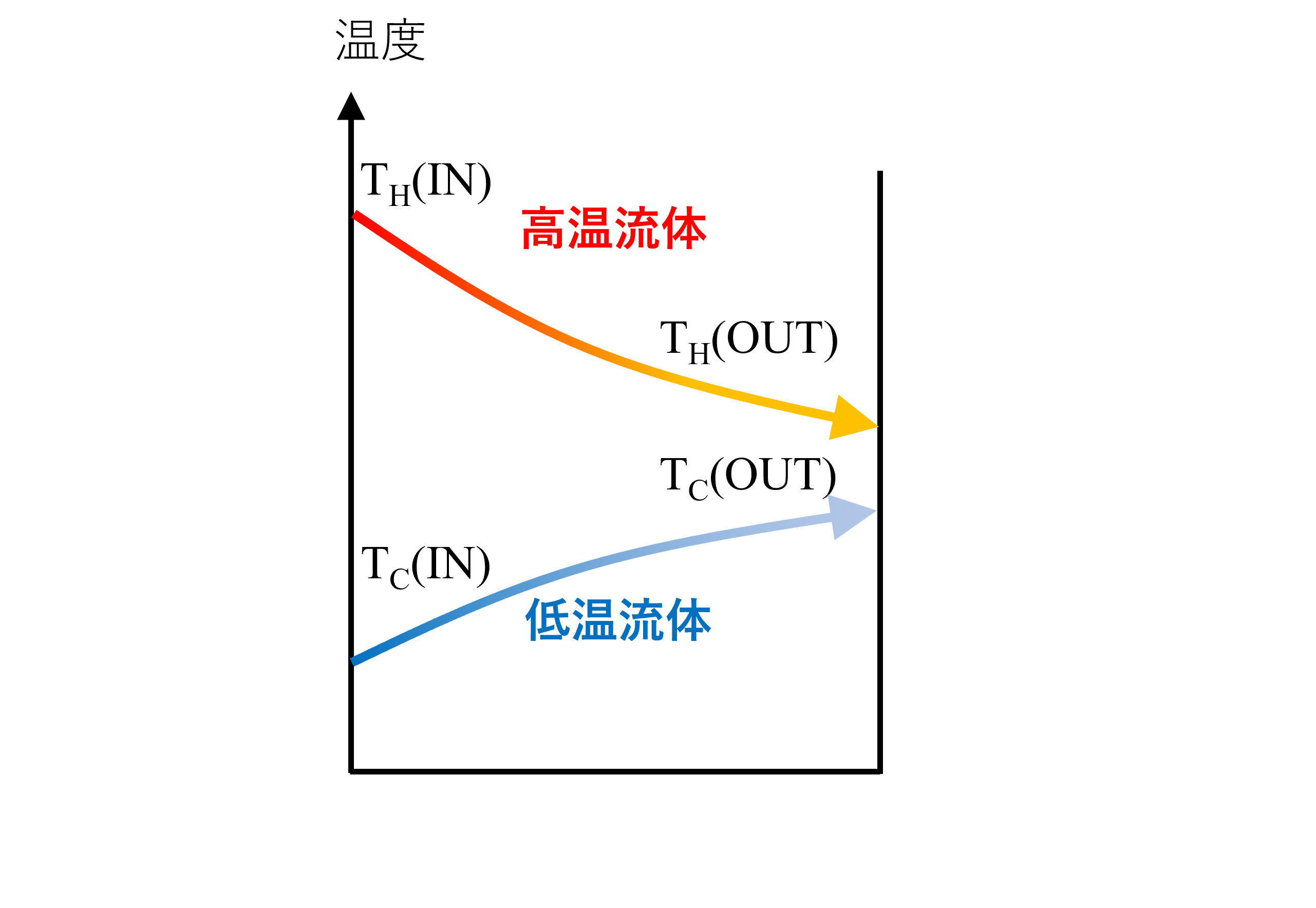
並流型熱交換器の場合
並流型は向流型よりも効率は低くなりますが、二重管による加温などではスペースの都合で並流型の熱交換を行うこともあります。
LMTD（対数平均温度差）とは？基本の仕組みをわかりやすく解説
対数平均温度差の定義と意味
早速結論ですが、対数平均温度差（LMTD、$\Delta{T}_{\text{LM}}$）は、入口側と出口側の温度差を$\Delta{T}_1$、$\Delta{T}_2$としたとき、「$\Delta{T}_{\text{LM}}=(\Delta{T}_1－\Delta{T}_2)÷\ln(\Delta{T}_1/\Delta{T}_2)$」という式で求められます。
このページの後半ではLMTDの導出手続きをご紹介します
LMTD（対数平均温度差）は、熱交換器で2つの流体が熱をやり取りする際に生じる温度差の平均値を、より正確に表現するための指標です。熱交換器内では、流体の温度差が一定でないため、単純な平均ではなく、特殊な（対数を使った）平均値が必要となります。
特に、向流型は温度差が大きく変わるため、LMTDの理解は伝熱計算の基礎となります。
算術平均温度差との違い・比較
算術平均温度差（AMTD）は、単純に入口と出口の温度差の平均を取る方法ですが、LMTDは温度差の変化を対数的に考慮します。
残念ながら、AMTDでは温度差が大きく変化する場合では正確な熱伝達量からの誤差が大きくなります。
| 項目 | LMTD（対数平均温度差） | AMTD（算術平均温度差） |
|---|---|---|
| 計算方法 | $(\Delta{T}_1－\Delta{T}_2)÷\ln(\Delta{T}_1/\Delta{T}_2)$ | $(\Delta{T}_1+\Delta{T}_2)÷2$ |
| 適用範囲 | 温度差が大きく変化する場合も正確 | 温度差がほぼ一定の場合のみ有効 |
| 計算精度 | 高い | 低い |
向流型熱交換器のLMTD計算を詳しく解説
実際に、向流型熱交換器でのLMTD（対数平均温度差）の計算をやってみましょう。
今回は高温オイルの入口温度が90℃、出口温度が50℃、冷却水の入口温度が5℃、出口温度が25℃の場合を考えます。
まず、各端の温度差を求めましょう。向流型熱交換器の場合、ΔTH＝高温流体入口－低温流体出口、ΔTC＝高温流体出口－低温流体入口です。
そのため、今の場合、ΔT1＝90−25＝65℃、ΔT2＝50−5＝45℃です。
$\Delta{T}_{\text{LM}}={\Delta{T}_1-\Delta{T}_2}/{\ln(\Delta{T}_1/\Delta{T}_2)}$へ代入します。
今の場合、$\Delta{T}_{\text{LM}}=(65-45)/\ln(65/45)=54.38^\circ\text{C}$と計算できます。
このように、熱交換器途中での温度差はわからなくても、LMTDは出入口での温度差だけで計算することができます。
計算機にいろいろな値を入れてLMTDを計算してみてください
LMTDの熱交換器での活用と設計ポイント
熱交換器におけるLMTDの役割
熱交換器では、LMTD($\Delta{T}_\text{LM}$)を使って伝熱量$Q$や必要な熱交換面積$A$を計算します。
たとえば、LMTD($\Delta{T}_\text{LM}$)が分かっている場合、熱交換器での伝熱量$Q$は「$Q=U\times{A}\times\Delta{T}_\text{LM}$」で求められます。ここで、$U$は総括伝熱係数です。
逆に、必要となる伝熱量$Q$が分かっている場合、「$A＝Q÷(U\times{\Delta{T}_\text{LM}})$」で伝熱面積$A$を設計できます。
- 伝熱量$Q=U\times{A}\times\Delta{T}_\text{LM}$
- 必要面積$A＝Q÷(U\times{\Delta{T}_\text{LM}})$
LMTDが求められれば、熱交換器の設計や性能確認が可能となります。
このように、LMTDは設計段階だけでなく、運用やトラブルシューティングにも欠かせない指標です。
向流型・並流型・マルチパス型の違いと設計への影響
熱交換器には、向流型、並流型、プレート式などさまざまな型式があります。
向流型は2つの流体が逆方向に流れるため、LMTDが大きくなり効率的な熱交換が可能です。一方、並流型は同じ方向に流れるため、LMTDが小さくなりやすく、設計時には面積を大きく取る必要があります。省スペースとされるマルチパス型は補正係数を用いてLMTDを調整する場合があります。
| 型式 | LMTDの特徴 | 設計への影響 |
|---|---|---|
| 向流型 | LMTDが大きい | 効率的な熱交換が可能 |
| 並流型 | LMTDが小さい | 面積が大きくなりやすい |
| マルチパス型 | 補正係数が必要 | 設計が複雑 |
LMTDを使うと熱交換量が計算できる証明
最後に、向流型熱交換器について$\Delta{T}_{\text{LM}}$を使うと、熱交換量が$Q=U\times{A}\times\Delta{T}_\text{LM}$で計算できる理由を紹介します。
別のページでは、マルチパス型の熱交換器に関する証明も行っていますので、是非ご覧ください。
全伝熱量を流体の温度差で表す
まず、熱交換器全体を通して考えましょう。
高温流体が入口温度$T_H(入口)$から出口温度$T_H(出口)$まで低下した場合、取り除かれた熱量は$Q=M_HC_H(T_H(入口)-T_H(出口))$と書けます。（$M_H$は流量、$C_H$は比熱）
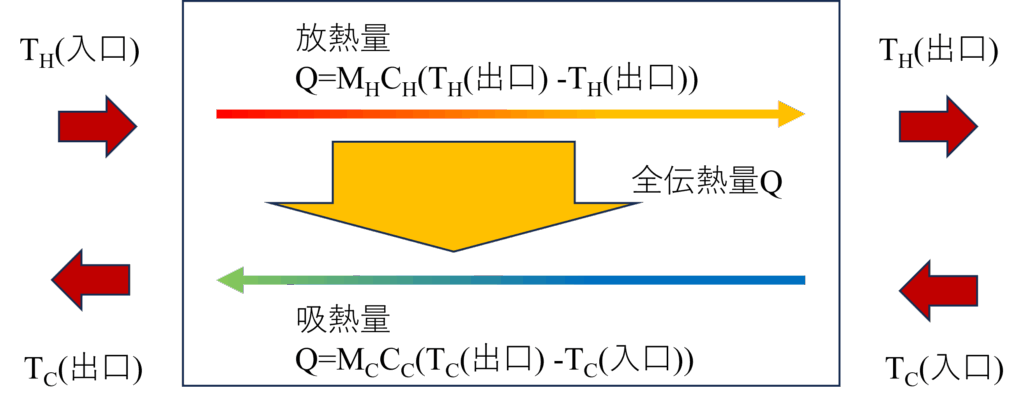
同じように低温流体に与えられた熱量は$Q=M_CC_C(T_C(出口)-T_C(入口))$とできるので、2つの式を変形すると、$\frac{1}{M_HC_H}-\frac{1}{M_CC_C}=\frac{1}{Q}(\Delta{T_H}-\Delta{T_C})$が得られます。（ここで、$\Delta{T}_H=T_H(入口)-T_H(出口)$、$\Delta{T}_C=T_C(入口)-T_C(出口)$と置いています）
なお、エネルギー保存式だけでは、$\Delta{T}_H$と$\Delta{T}_C$の関係式しか分かりません。具体的な熱交換量を知るためには面積当たりの熱交換量から全伝熱量を表す式を立てる必要があります。
エネルギー保存式だけだと、交換熱量が$20\text{J/s}$でも$200\text{MJ/s}$でも可能だからね
面積当たりの熱交換量から全伝熱量を計算する
次に、面積当たりの熱交換量$\text{d}Q$から全伝熱量$Q$の表式を導きましょう。
微小面積$\text{d}A$における交換熱量$\text{d}Q$を考えましょう。$\text{d}A$における温度差$T_H-T_C$を${\Delta}T$とすると、交換熱量は$\text{d}Q=U\Delta{T}\text{d}A$と書けるはずです。$U$は面積・時間・温度差当たりの熱交換量（いわゆる総括伝熱係数）です。
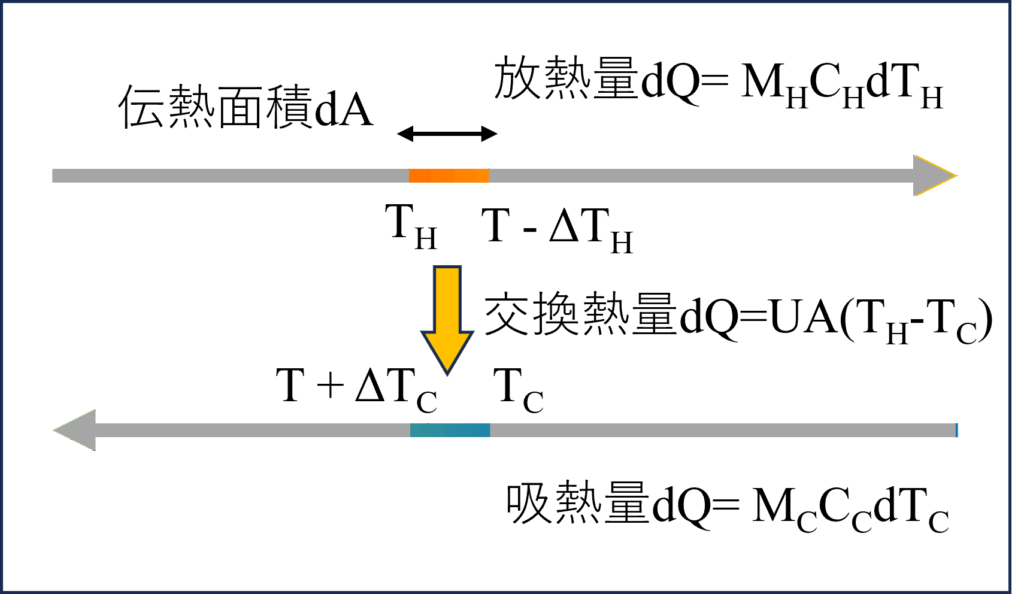
この区間で高温流体は$\text{d}T_H$だけ温度が下がり、低温流体は$\text{d}T_C$だけ温度が上がるとしましょう。すると、高温流体が失った熱量は$\text{d}Q=M_HC_H\text{d}T_H$、逆に低温流体が受け取った熱量は$\text{d}Q=M_CC_C\text{d}T_C$と表せるので、この2式を変形すると、$\text{d}(\Delta{T})=\text{d}Q\Bigl(\frac{1}{M_HC_H}-\frac{1}{M_CC_C}\Bigl)$を得ることができます。（ここで、$\text{d}(\Delta{T})=\text{d}T_H-\text{d}T_C$と置いています）
したがって、黄色線の2式から$\text{d}Q$を消去すると$U\text{d}A\Bigl(\frac{1}{M_HC_H}-\frac{1}{M_CC_C}\Bigl)=\frac{\text{d}(\Delta{T})}{\Delta{T}}$が得られ、熱交換器入口から出口まで積分すると、$UA\Bigl(\frac{1}{M_HC_H}-\frac{1}{M_CC_C}\Bigl)=\ln\frac{\Delta{T}_H}{\Delta{T}_C}$が得られます。
向流熱交換器の伝熱量の表式を得る
最後に、黄色線の2式（$\frac{1}{M_HC_H}-\frac{1}{M_CC_C}=\frac{1}{Q}(\Delta{T_H}-\Delta{T_C})$と$UA\Bigl(\frac{1}{M_HC_H}-\frac{1}{M_CC_C}\Bigl)=\ln\frac{\Delta{T}_H}{\Delta{T}_C}$）を利用すると、向流熱交換器の伝熱量の表式$Q=UA\frac{\Delta{T}_H-\Delta{T}_C}{\ln(\Delta{T}_H/\Delta{T}_C)}$を得ることができます。
まとめ
このページでは、向流熱交換器と並流熱交換器における対数平均温度差$\Delta{T}_{\text{LM}}$を具体的に計算してもらいつつ、熱交換器の基本式が$Q=UA\Delta{T}_{\text{LM}}$になる理由まで解説しました。
実際の工場でも$Q=AU\Delta{T}_{\text{LM}}$の式を使って、流体の出入口温度を用いて$U$値の管理を行い、「生産性を上げられる余地がないか？」や、「tubeの汚れ増大傾向がないか？」などを確認しています。
熱交換器では場所によって流体温度が変化するので、熱交換器での伝熱を考える際は必ず対数平均温度差$\Delta{T}_{\text{LM}}$の概念を使うようにしましょう。