プラントル数(Pr数)は粘性拡散と熱拡散の比を表す値で、要するに熱を伝えやすい物質かどうかが分かる値で、Pr=1が境目です。
残念ながら、私はプラントル数を初めて教わったとき、物質の固有値であるプラントル数が具体的にどのように役立つか分かりませんでした。こんな出どころがよくわからない無次元量を考えて意味ないでしょ?って思ってました。
しかし、実はプラントル数はヌセルト数などとの関係式がいくつも提唱されており、熱交換器などの設計には欠かすことができないものです。このページでは、プラントル数の本質的な意味や、実務での活かし方まで分かるように、水や油のプラントル数から熱交換器における計算例まで、幅広く解説します。
プラントル数とは?-基本の意味と流体工学での重要性をわかりやすく解説
プラントル数の定義と役割
さて、早速ですが、プラントル数($\text{Pr}$数)は$\text{Pr}={\mu{c_p}}/{k}$で定義される値です。重要なことですが、単位はありません。なお、$\mu$は粘度、$c_p$は比熱、$k$は熱伝導率です。

プラントル数には次元がない無次元量だね。

無次元量だからこそ、長さや重さに影響されないというメリットがあります。
流体の情報
プラントル数は、空気や水などの一般的な流体では1前後ですが、油などは10以上、液体金属は0.01以下と大きく異なります。

プラントル数を使うことで、流体の性質を簡潔に表現することができるんだね。
| 流体 | プラントル数(Pr) |
|---|---|
| 空気 | 約0.7 |
| 水 | 約7 |
| 油 | 10~1000 |
| 液体金属 | 0.01以下 |
プラントルは数$\text{Pr}={\mu{c_p}}/{k}$定義されているので、流体の粘度$\mu$、熱伝導率$k$、比熱$c_p$の物性値に大きく依存します。
設計や解析では正確な物性値を用いることが重要なので、実際の熱交換器の設計等では、内部での温度や圧力の違いによる物性値の変化も考慮する必要があります。
なぜ熱伝達や冷却設計に使われるのか
プラントル数とは、境界層外の流れに対して、どの程度厚く温度、速度境界層が発達するかを示す指標です。
プラントル数が大きい場合、流体の温度境界層は速度境界層より薄くなります。すなわち流体が効率的に熱交換できることを表しています。逆に小さい場合は、熱交換には不利です。
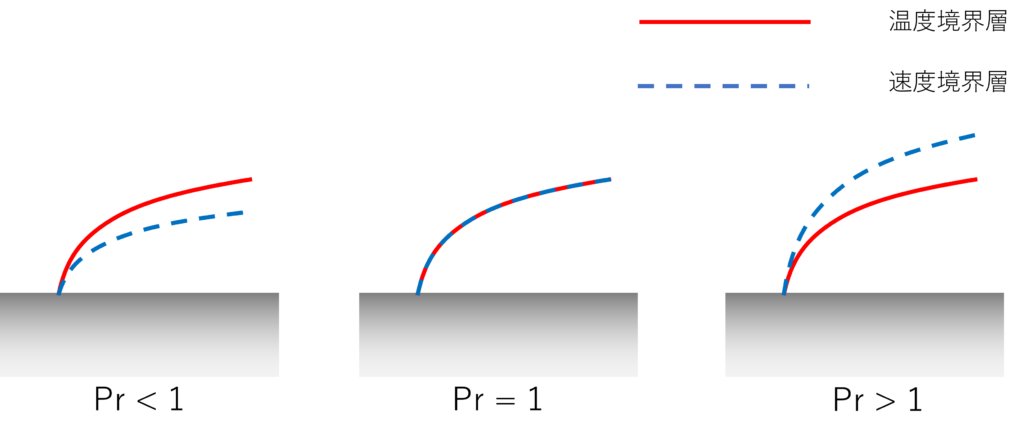

「境界層」とはその中で温度や流速が急激に変化する層のことです。

例えば冷たい壁沿いに高温流体が流れている場合は、「温度境界層」で流体温度が急に変わるんだね
例えば、$\text{Pr}$数が大きい油などは、粘度が高いため、流体が伝熱面に長くとどまってくれるので、熱伝達が効率的に行われます。逆に$\text{Pr}$が小さい空気や液体金属などは、熱を効率的に伝えることができません。
つまり、プラントル数$\text{Pr}={\mu{c_p}}/{k}$は流体の運動量拡散(粘性拡散とも呼ばれる)と熱拡散のどちらが優勢かを表しています。

熱伝導率$k$が高い流体は熱を効率よく伝え、粘度$\mu$が高い流体は運動量の拡散が遅くなります。
ヌセルト数・レイノルズ数との関係式まとめ
ヌセルト数・レイノルズ数・プラントル数の関係式とは?
プラントル数$\text{Pr}$は、ヌセルト数$\text{Nu}$やレイノルズ数$\text{Re}$と密接な関係があり、$\text{Nu}=C\times\text{Re}^m\times\text{Pr}^n$という形で表されます。($C$、$m$、$n$は流れの状態や流路の形状によって異なります。)

ヌセルト数$\text{Nu}$は、対流による熱伝達と伝導による熱伝達の比を表していて、レイノルズ数$\text{Re}$は流れの性質(層流・乱流)を表すよね。
これらプラントル数の関係式は流体の熱伝達特性を定量的に評価し、工業的な設計をするための基礎となっています。
| 状況 | プラントル数の関係式 | 名称 |
| 円管内、強制対流、乱流 | $\text{Nu}=0.023\text{Re}^{0.8}\text{Pr}^{0.4}$ | Ditus-Boelterの式 |
| 円管内、強制対流、層流 | $\text{Nu}=1.86(\text{Re}\cdot\text{Pr})^{\frac{1}{3}}\Bigl(\frac{d}{L}\Bigl)^{\frac{1}{3}}\Bigl(\frac{\mu}{\mu_\infty}\Bigl)^{0.14}$ | Sieder-Tateの式 |
| 平板上、強制対流、乱流 | $\text{Nu}=0.036\text{Re}^{0.8}\text{Pr}^{\frac{1}{3}}$ | |
| 球外面、強制対流 | $\text{Nu}=2.0+0.6\text{Re}^{\frac{1}{2}}\text{Pr}^{\frac{1}{3}}$ | Ranz-Marshallの式 |
| 垂直平板、自然対流、乱流 | $\text{Nu}=0.129(\text{Gr}\cdot\text{Pr})^{\frac{1}{3}}$ | |
| 垂直平板、自然対流、層流 | $\text{Nu}=0.555(\text{Gr}\cdot\text{Pr})^{\frac{1}{4}}$ |
プラントル数の関係式は、流れ場の形状や流体の流れ方によって異なります。また、Sieder-Tate式における$L$は円管の長さ、$\mu$は円管内流体の粘度(算術平均)、$\mu_\infty$は壁温度での粘度です。

実際に、円管内の流れと平板上の流れでは、境界層の発達や熱伝達のメカニズムが異なるため、適用するべき式も変わります。
このように、流れ場ごとに最適な関係式を選ぶことが、正確な熱伝達率の推定には不可欠です。
最も有名なプラントル数の関係式
プラントル数の関係式で最も有名なものは、円管内の乱流におけるDittus-Boelterの式$\text{Nu}=0.023\text{Re}^{0.8}\text{Pr}^{0.4}$です。これは熱交換器における設計などで幅広く活用されています。
Dittus-Boelterの式によって見積もられた熱伝導率は実際よりも小さくに見積もるとされており、例えばSaniによって水の伝熱率とDittus-Boelterの式が比較されています。(R.L.Sani; Downflow boiling and non-boiling heat transfer in a unformly heated tubes, USAEC Rep. UCRL-9023, 1960.)


Dittus-Boelterの式が実際よりも伝熱率を低く見積もることは、設計の観点からは安全サイドになります。
プラントル数の求め方・計算手順-わかりやすく解説
基本問題
簡単な計算例として、トルエンのプラントル数を求めてみましょう。
- 粘度$\mu$(mPa・s) :0.56
- 比熱$c_p$(kJ/kg・K) :1.68
- 熱電率$k$(kJ/m・hr・K):0.54

ポイントは各物性値をSI単位系の基本であるm・kg・sの値に変えることです。
粘度は今単位が(mPa・s)になっているので、(Pa・s)に変えると$\mu=0.56/1000=0.00056$(Pa・s)になります。
比熱は(kJ/kg・K)になっているので、(J/kg・K)に変えると$c_p=1680$(J/kg・K)になります。
熱電率は(kJ/m・hr・K)になっているので、(J/m・s・K)にかえると$k=540/3600=0.15$(J/m・s・K)になります。
プラントル数($\text{Pr}$数)は$\text{Pr}=\frac{\mu{c_p}}{k}$で定義されるので、トルエンの場合、$\text{Pr}=\frac{0.00056\times1680}{0.15}=6.27$と計算することができます。
応用問題
次に、熱交換器のtubeを流れるトルエンの伝熱係数$h(\text{kJ/m}^2\cdot\text{hr}\cdot\text{K})$を求める計算例を紹介します。
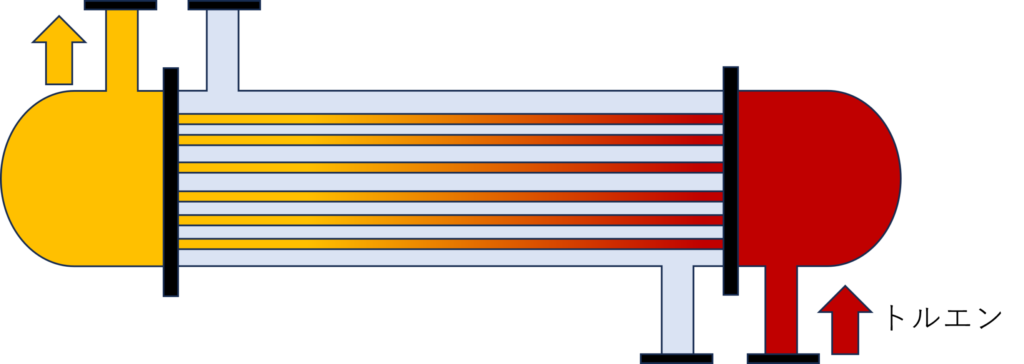
熱交換器の条件
- tube総数は150本
- tube内径は2.5cm
- トルエン(tube側)の流量は50ton/hr
トルエンの物性値($20^\circ\text{C}$)
- 密度$\rho$(kg/m3) :860
- 粘度$\mu$(mPa・s) :0.56
- 比熱$c_p$(kJ/kg・K) :1.68
- 熱電率$k$(kJ/m・hr・K):0.54
伝熱係数を計算するためには、tube内でトルエンが流れる流速を知る必要があります。そのため、まずはトルエンが流れるtubeの総断面積を求めましょう。
今回はtubeが150本あり、tube内径は$2.5\text{cm}(0.025\text{m})$なので、総断面積は$\pi\times0.025^2/4\times150=0.07363\text{m}^2$です。
tube総断面積が分かったので、tubeを流れるトルエンの流速とレイノルズ数を求めましょう。
トルエンは50ton/hrで流すので、tube内を流れるトルエンの流速は$(50\times10^3/3600)/(860\times0.07363)=0.2193\text{m/s}$になります。
したがって、レイノルズ数は$\text{Re}=\frac{860\cdot0.2193\cdot\frac{2.5}{100}}{\frac{0.45}{1000}}=10479$となります。
いよいよ、DittusDittus-Boelterの式$\text{Nu}=0.023\text{Re}^{0.8}\text{Pr}^{0.4}$を利用して、伝熱係数$h$を求めます。
いまレイノルズ数は$\text{Re}=10479$で、トルエンのプラントル数は$\text{Pr}=\mu{c_p}/k=6.27$なので、$\text{Nu}=0.023\text{Re}^{0.8}\text{Pr}^{0.4}=78.86$になります。
ヌセルト数$\text{Nu}=hD/k$の定義により、伝熱係数は$h=\text{Nu}\frac{k}{D}=78.86*0.15/0.025=1703\text{kJ/m}^2\cdot\text{hr}\cdot\text{K}$になります。
まとめ|プラントル数を実務に活かすには
このページでは、プラントル数の本質的な意味や、実務での活かし方まで分かるように、物理的な意味から熱交換器における計算例まで、幅広く解説しました。
物質固有値であるプラントル数(Pr数)は流れの状態を表すヌセルト数$\text{Nu}$やレイノルズ数$\text{Re}$などとの関係式がいくつも提唱されており、熱交換器などの設計に欠かすことができない値になっています。
伝熱係数を知りたい際は、プラントル数の関係式がすでに提唱されている場合はそれらを積極的に利用し、関係式がない場合に流動シミュレーションなどを利用するようにしましょう。


