散らかった部屋を見て「エントロピー増えたなぁ」とか言ったりしませんか?エントロピー増大の法則はよく耳にする法則ですが、きちんと理解しようとすると難しいと感じやすいシロモノです。

大学の授業では小一時間かけてエントロピー増大の法則を導く講義を行いますが、残念ながら私は「エントロピー増大の法則は難しい」という考えに陥りました。
このページでは、「エントロピー増大の法則は実は簡単」と感じてもらうため、ΔS>0からシンプルな道筋でコーヒーが冷めることと、車が摩擦で止まることをご紹介します。
低温から高温へは熱は移動しない【クラウジウスの法則とも言う】
エントロピー増大の法則に対する超シンプルな回答
エントロピー増大の法則とは「熱は高温から低温へ移動する」ということに尽きます。それ以上でもそれ以下でもありません。

クラウジウスの法則だね

つまり、「エントロピー増大の法則ってなに?」と聞かれたら、「熱いコーヒーは冷めることだ」と答えられれば、エントロピー増大の法則を完璧にマスターできていることになります。
あまりに当たり前すぎて、「素人の知ったかぶりかよ」とは思ってはなりません。むしろ「こいつ、完璧にエントロピー増大の法則を理解してやがる」と思わなければなりません。

数式でも確認しよう
「部屋($T_{部屋}$)に置いたコーヒー($T_{コーヒー}$)は冷める」ことをエントロピー増大の法則$\Delta{S}>0$から説明できることを見ていきましょう。

いま、奇跡が起きて部屋の空気からコーヒーに熱${\Delta}Q$が移動したとします。この場合、コーヒーのエントロピー変化量は$\Delta{S}_{コーヒー}=\frac{{\Delta}Q}{T_{コーヒー}}$となり、部屋のエントロピー変化量は$\Delta{S}_{部屋}=-\frac{{\Delta}Q}{T_{部屋}}$となります(空気からは熱が出ていくのでマイナス符号に注意)。

エントロピー変化量$\Delta{S}$は移動熱量$\Delta{Q}$と温度$T$から$\Delta{S}=\Delta{Q}/T$で求められることを利用しています
つまり、全体としてのエントロピー変化は部屋とコーヒーのエントロピー変化を合計して$\Delta{S}=\frac{{\Delta}Q}{T_{コーヒー}}-\frac{{\Delta}Q}{T_{部屋}}=\frac{{\Delta}Q}{T_{コーヒー}T_{部屋}}({T_{部屋}}-{T_{コーヒー}})$となります。$T_{部屋}<T_{コーヒー}$なので、部屋の空気からコーヒーに熱が移動すると$\Delta{S}<0$となってしまい、エントロピー増大の法則と矛盾します。つまり、「エントロピー増大の法則からコーヒーはひとりでに熱くはならない」と言えるのです。
熱を全て仕事に変えるサイクルは不可能【トムソンの法則とも言う】
エントロピー増大の法則のもう一つの言い換え
エントロピー増大の法則は「熱を全て仕事に変えるサイクルは無い」とも言えます。

トムソンの法則だね

永久機関はトムソンの定理に反するものが多いです
もし、熱を全て仕事に変えるサイクルができると、例えば車が走ったときに発生した摩擦熱を100%再利用することで、永久に走る車を作ることができるようになったりします。(当然、ムリです。)

数式でも確認しよう
エントロピー増大の法則$\Delta{S}>0$から「熱を全て仕事に変えるサイクルは無い」を導けることを確かめましょう。
「熱源」から熱$Q$が「熱サイクル」に入って、全て仕事$W$へ変換されたとします。
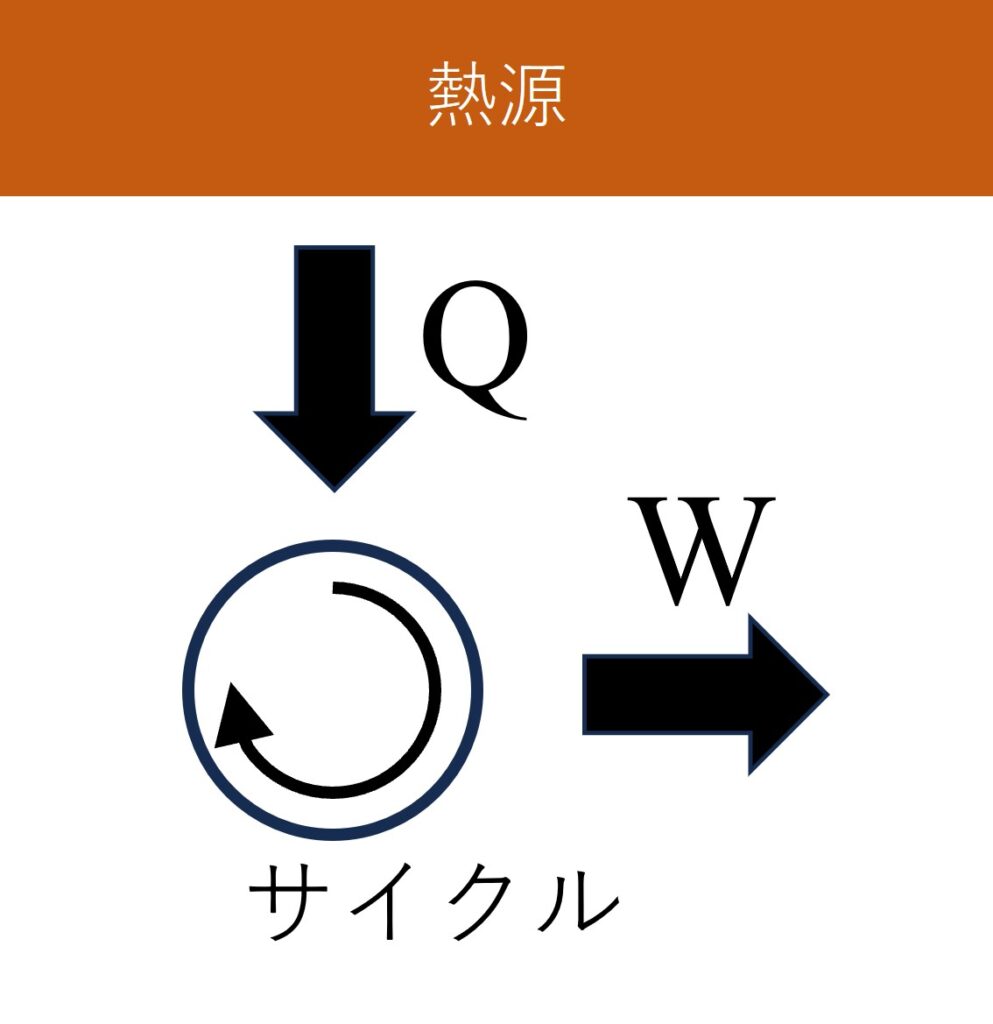

エントロピーは「熱サイクル」と「熱源」全体の寄与を足し合わせて考える必要があるので、まずは「熱サイクル」のエントロピー変化を調べましょう。
「熱サイクル」はサイクルが1周すると状態(例えばピストンの位置や気体の温度)が元の状態に戻ります。なお、エントロピーは状態が1つに決まると、値が1つに定まる「状態量」です。そのため、熱サイクルが1周した前後でエントロピー変化は無いので$\Delta{S}_{\text{熱サイクル}}=0$です。
一方の「熱源」のエントロピー変化を考えてみましょう。温度$T$の熱源から熱量${\Delta}Q$が出たとすると、エントロピー変化は$\Delta{S}_{\text{熱源}}=-\frac{{\Delta}Q}{T}$となります。(熱源からは熱が流出しているので、マイナス符号がつきます)
結局、「熱サイクル」と「熱源」全体のエントロピー変化は$\Delta{S}=\Delta{S}_{\text{熱サイクル}}+\Delta{S}_{\text{熱源}}=-\frac{{\Delta}Q}{T}<0$となります。つまり、「熱を全て仕事に変える熱サイクル」はエントロピー増大の法則$\Delta{S}>0$に反するから「永久機関は存在しない」という結論になるのです。
【言い間違え注意】「熱を全て仕事に変えられない」は誤り?
よく「熱は全て仕事に変えられない」という表現を聞きますが、実はこれは誤りです。
トムソンの原理は「熱源から受けとる熱と等量の仕事を行い、他に何の変化も残さない過程は実現できない。」とされます。この「他に何の変化も残さない過程」というものがクセモノなのです。
じつは、変化を残せば、熱を全て仕事に変えることは可能です。その最たる例が断熱膨張です。高温の気体を断熱的に膨張させることで非常に簡単に熱を全て仕事に変えることができます。

「熱は全て仕事に変えられない」と聞いて「断熱膨張では熱を全て仕事に変えられているよ」と意見するのは揚げ足取りだよ。。。

テストで変な減点をとられないように注意しましょう
まとめ
このページでは、「エントロピー増大の法則は実は簡単」と感じてもらうため、ΔS>0からシンプルな道筋でコーヒーが冷めることと、車が摩擦で止まることが分かることをご紹介しました
なお、大学の授業で行うようなエントロピー増大の法則を様式美のように導く手続きに関しては別のページでご紹介していますので、そちらもご覧ください。
また、「インクが広がる」や「部屋が散らかる」は統計力学的なエントロピー$S_{\text{統計}}$と熱力学的なエントロピー$S_{\text{熱}}$が同じであることをまず確かめる必要があります。$S_{\text{統計}}=S_{\text{熱}}$に関しては、こちらのページをご覧ください。

