「膨張率」とは温度変化に伴う物質の体積変化を表すものです。特に窒素などの気体の場合、膨張率βはほとんど温度Tだけで計算できます。
私は、理想気体の膨張率がβ=1/Tで表されることは分かるけど、実在気体(窒素や二酸化炭素など)は胴なんだよ?という疑問を持っていました。
このページでは、理想気体の膨張率β=1/Tの証明だけでなく、窒素や二酸化炭素、ヘリウムなどの膨張率が理想気体からどの程度外れるかまで調べたものをご紹介します。
気体の体積膨張率β=1/Tは本当?成立条件を温度・圧力から解説
膨張率とは?気体・液体・固体での定義と「熱膨張率」の基本
膨張率(熱膨張率)は、温度が変わったときに物体の「長さ」や「体積」がどれだけ増減するかを表す指標です。固体では棒や板のように「長さの変化」が扱いやすいため線膨張率がよく使われ、液体・気体では容器内で形が定まらないため「体積の変化」を表す体積膨張率(体膨張率)が中心になります。
特に気体は分子間距離が大きく、温度上昇で体積が大きく変わりやすいので、固体・液体より膨張率が大きいのが一般的です。また、気体の膨張は「圧力$P$や温度$T$を一定に保つ」など条件を決めないといけません。
膨張率βの定義と理想気体の式からβ=1/Tを導く
膨張率(膨張係数)では、代表的なのが、体積膨張率$\beta$(ベータ)で、温度変化に対してどれだけ体積が変わるかを示します。

いろいろな物質の$\beta$を計算してみましょう
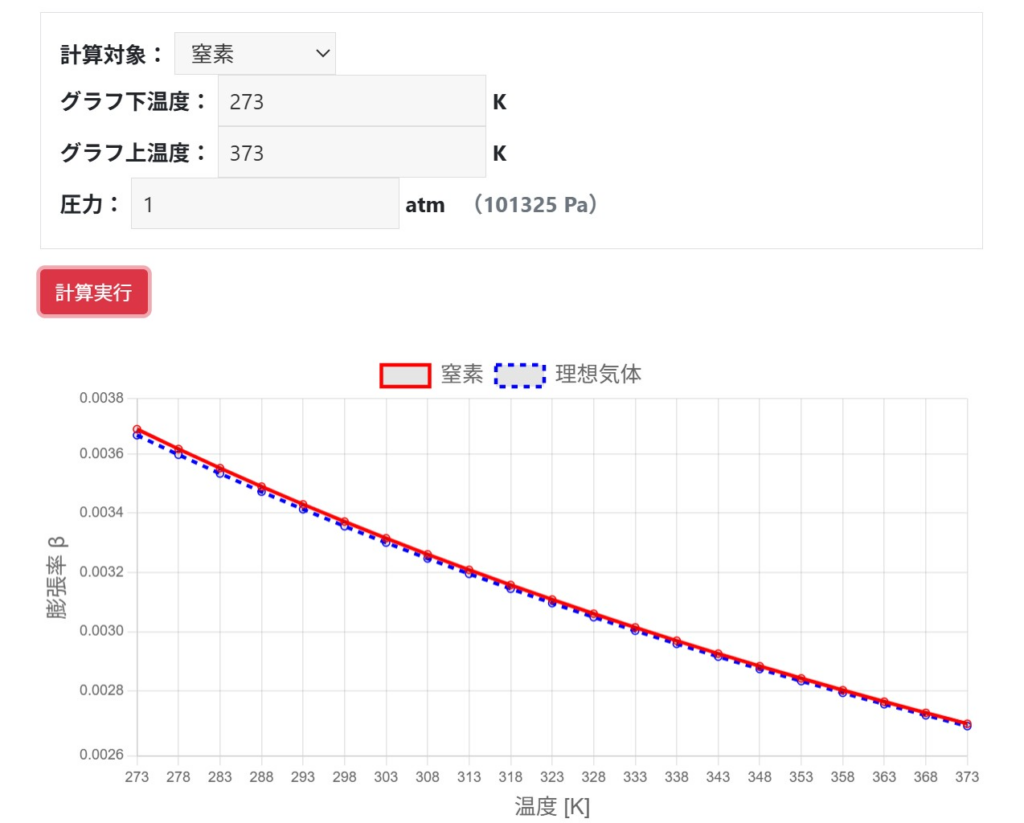
さて、結論から言うと、$\beta=1/T$は「理想気体」で体積膨張率$\beta$を定義した場合に成り立ちます。このときβは圧力$P$に依らず温度$T$だけで決まり、たとえば$T=273.15\text{K}$付近では$β≒1/273.15≒0.00366\text{K}^{-1}$となります。
一方、実在気体では分子間力や分子の体積の影響で理想気体の式から外れますが、大気圧で室温の条件では$\beta$が理想気体から大きく外れることはありません。

普通の条件では実在気体でも$\beta=1/T$と扱ってもほぼ問題ないんだね。
理想気体の式から導く:β=1/T
では、理想気体の$\beta=1/T$を導いてみましょう。利用するのは、理想気体$1\text{mol}$の状態方程式、 $PV=RT$です。
状態方程式から$V=\frac{RT}{P}$なので、圧力$P$一定で温度$T$で微分すると、$(∂V/∂T)_P=R/P$となります。これを体積膨張率の定義$\beta=(1/V)(∂V/∂T)_P$に代入すると、$\beta=(P/RT)・(R/P)=1/T が得られます。

$V$で割っているのは、規格化のためです。

$V$で割らないと、大きな体積の時に膨張率が大きくなってしまうものね。
やはり理想気体では、体積膨張率$\beta$は温度$T$の逆数で決まり、圧力$P$には依存しません。
よくあるミス:単位換算、基準温度、定数の扱い(K・Pa・Lなど)
膨張率計算のミスは、ほぼ単位と基準の取り違えに集約されます。
特に多いのは、温度を℃のまま$T$に代入する、圧力をヘクトパスカル単位のまま状態方程式に入れる、体積を$L$と$m^3$で混在させる、の3つです。
また「β≈1/273」という有名な値は0℃付近の近似であり、常温では1/293程度に変わります。
計算前に、TはK、Pは絶対圧(Pa)、Vはm^3、Rは8.314(J/(mol·K))か、比気体定数(J/(kg·K))か、を揃えるだけで事故は激減します。
- $T$は必ず$\text{K}$(ケルビン)で評価(T=℃+273.15)
- $P$は原則「パスカル」(SI単位系)
- $V$の単位は$\text{m}^3$(SI単位系)を使うと安全
実在気体(現実の気体)はなぜβ=1/Tからズレる?圧力・密度・相互作用
実在気体の体積膨張率が理想気体とどう違うか解説
実在気体は、1atm・室温では理想気体に近づきますが、高圧や低温ではPV=RTからずれます。

このずれは、分子間の引力(体積を小さく見せる方向)や分子自身の大きさ(体積を大きく見せる方向)などが原因です。
その結果、状態方程式が理想気体のPV=RTから外れるので、その結果、実在気体の$\beta$は$1/T$からずれます。
実在気体の状態方程式としてよく用いられるものがファンデルワールス状態方程式$P=\frac{RT}{V-b}-\frac{a}{V^2}$です。実は、簡単な計算を行うと、この状態方程式$P=\frac{RT}{V-b}-\frac{a}{V^2}$から、実在気体の膨張率として$\beta=\frac{1}{T}\Bigl(1-\frac{b}{T}\Bigl)/\Bigl[1-\frac{2a}{RTV}\Bigl(1-\frac{b}{T}\Bigl)^2\Bigl]$が得られます。

確かに、理想気体($a=b=0$)の時、$\beta=1/T$になるね
実在気体の$\beta$の導出はこちら

圧力が高い/温度が低いとズレやすい:蒸気・圧縮の観点
実在気体では、高圧になるほど分子間距離が縮まり、分子の体積や相互作用が無視できなくなるため、理想気体からのズレが増えます。
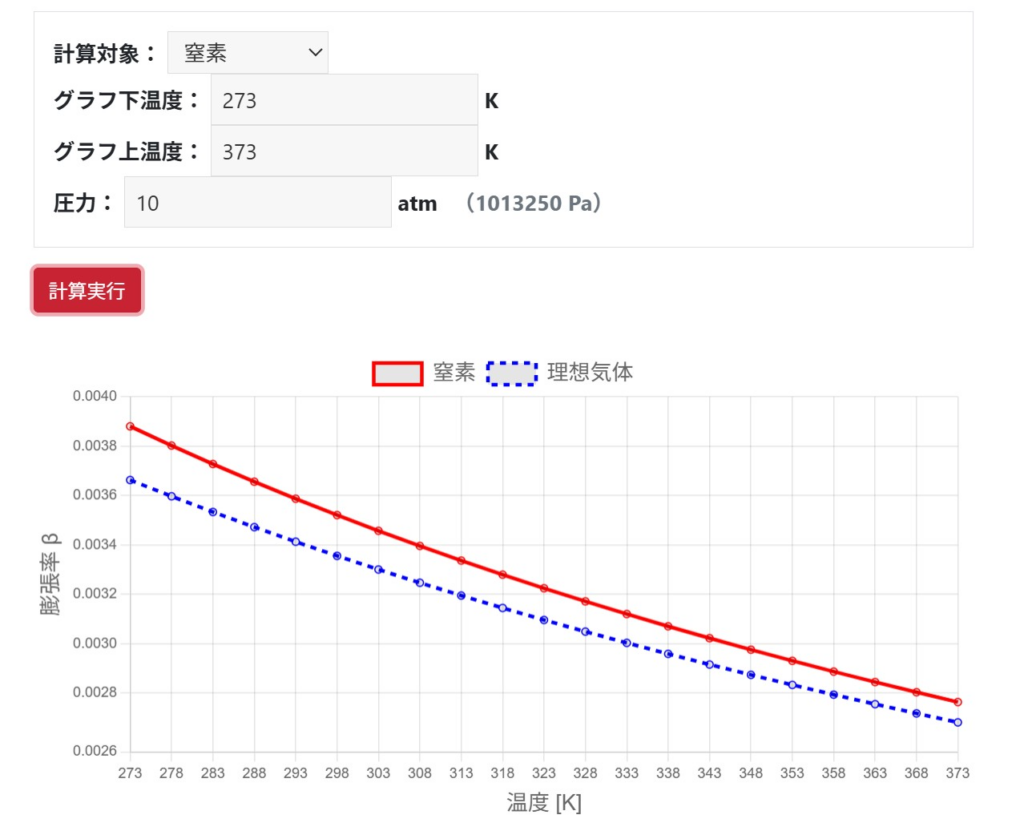
一方で、低温では分子運動が弱まり、引力の影響が相対的に強くなるため、やはり実在気体は理想気体からズレやすくなります。さらに、飽和蒸気に近い状態(凝縮しやすい領域)では、温度を上げたときの体積変化が単純な比例ではなくなり、β=1/Tのような単純式は危険です。
冷媒や水蒸気、CO2などは相図(臨界点・飽和線)を意識して、物性表や状態方程式(実在気体モデル)で評価するのが基本になります。特に圧縮機・高圧ボンベ・冷媒・CO2などは、理想気体近似が効きにくい領域があり、$\beta$を$1/T$で固定すると体積変化を過小評価・過大評価するリスクがあります。
まとめ:β=1/Tの使える範囲、実在気体の注意点、計算の最短手順
このページでは、理想気体の膨張率$\beta=1/T$の証明だけでなく、窒素や二酸化炭素、ヘリウムなどの膨張率が理想気体からどの程度外れるかまで調べたものをご紹介しました。
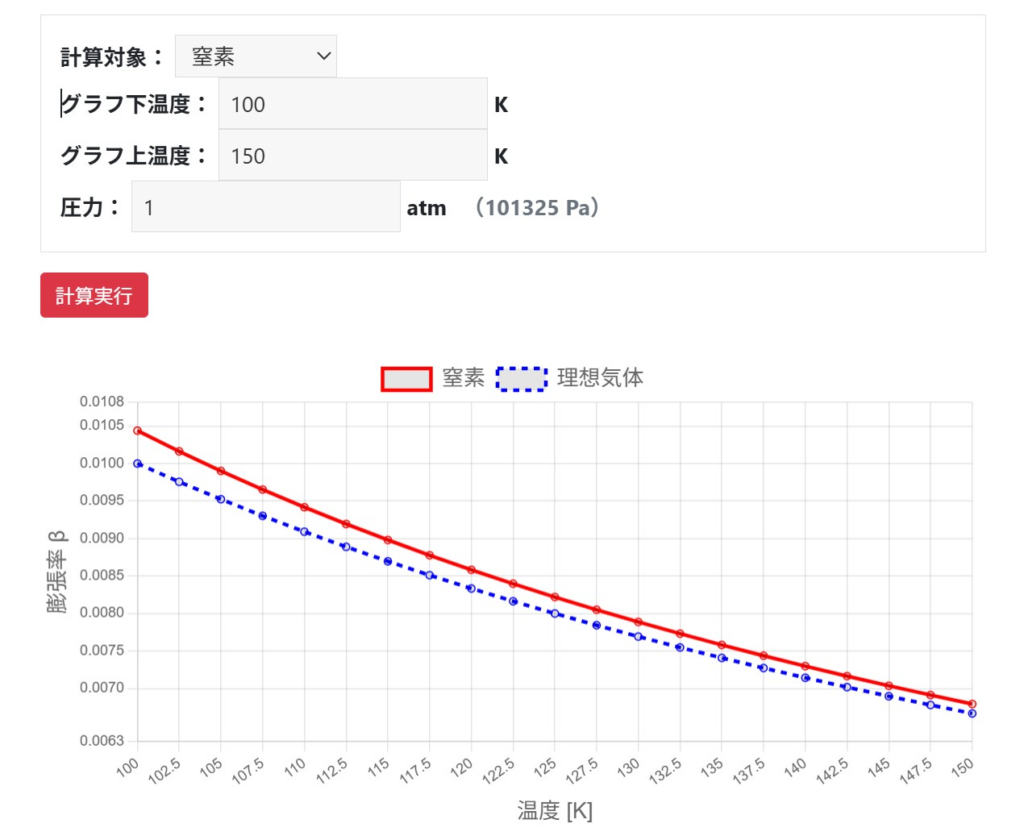
室温や大気圧程度の環境では、実在気体であっても$\beta=1/T$として膨張率を計算しても、実務上はあまり支障はありません。一方、10気圧のような高圧状態や、-150℃といった低温状態では$\beta=1/T$では膨張率を低く見積もるため危険です。
実在気体の膨張率を見積もりたくなった際は、このページにあるアプリケーションでいろいろな温度、圧力体での$\beta$を計算してみてください。

