大学の熱力学で教わる公式の中で最も覚えにくいのは「マクスウェルの関係式」ではないでしょうか?
圧力PやエントロピーSなどの関係式が4つもあり、さらにはプラスマイナスの符号まで正確に使う必要があり、かなり覚えにくい関係式です。
このページではマクスウェル関係式の覚え方を一つ紹介し、もし忘れてしまっても簡単にマクスウェルの関係式を作る方法を解説します。
【結論】「ポークで酢豚」で覚えよう
Maxwell関係式を最も簡単に覚えられる方法は、ずばり「ポークで酢豚」です。

これは私が大学時代に授業で教わった覚え方です

「ポークで酢豚」法では次の3ステップでMaxwell関係式を作ることができます。
- $P$を左下か右上に書く
- $P,S,V,T$(ポーク($P$)で酢豚($SVT$))の順で円状に書く
- $PSVT$が反時計回りなら$+$符号、時計回りなら$-$符号をつける
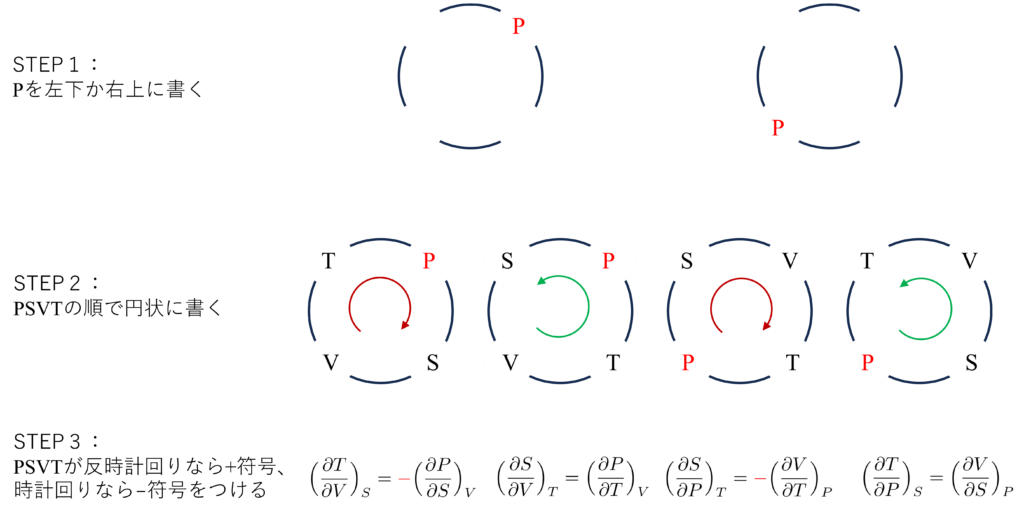
- 「$P$の配置(左下、右上)」と「$P,S,V,T$の描き方(時計回り、反時計回り)」が$2$通りずつあるので、Maxwell関係式は$2\times2=4$つ存在します。
- $PSVT$を書いたときの上下位置がMaxwell関係式の分子分母の関係に対応します。
- 偏微分記号の固定変数$\Bigl(\frac{\partial}{\partial}\Bigl)_\square$の$\square$には$PSVT$を円状に書いた時の下段文字が入ります。

$P$を左下か右上に配置しなければならないのはMaxwell関係式のプラスマイナスの整合性を合わせるためです
使用例
例えば、$\Bigl(\frac{\partial{T}}{\partial{P}}\Bigl)_S=\frac{TV\beta}{C_V}$を示す問題では、$\Bigl(\frac{\partial{T}}{\partial{P}}\Bigl)_S$に対してMaxwellの関係式を使う必要があります。
この際、まずは($P$が分母なので)$P$を左下に書き、($T$が分母なので)$T$が上段にくるように$PSVT$を円状に書きましょう。
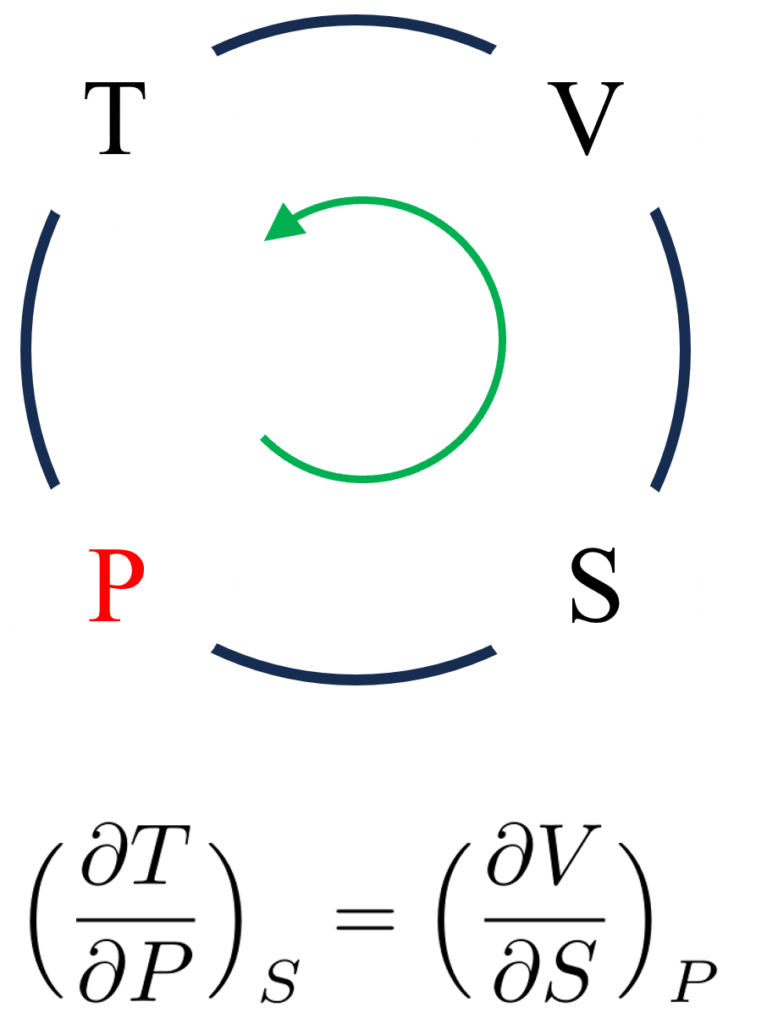
さらに$PSVT$(ポークで酢豚)が反時計回りなので、符号は$+$になります。つまり、Maxwellの関係式の1つ$\Bigl(\frac{\partial{T}}{\partial{P}}\Bigl)_S=+\Bigl(\frac{\partial{V}}{\partial{S}}\Bigl)_P$を書き下せます。
【保険】プラスマイナスが分からなくなったときは
Maxwellの関係式でもっとも覚えにくいのは「プラスマイナス」の関係でしょう。
「PTSV(ポークで酢豚)を円状に描く」ことはなかなか忘れにくいですが、「$P$を左上に配置するべきなのか?右上でもよいのか?」「時計回りがプラス?それともマイナス?」とMaxwell関係式のプラスマイナスに直結する部分を忘れてしまいがちです。

大学のレポートだと都度調べられるけど、定期試験や大学院試では当然インターネット検索できない。。

「ポークで酢豚」を忘れた場合でも、試験中にMaxwell関係式を簡単に作り出す方法も保険として紹介します。
Maxwell関係式を一から簡単に作る方法は「熱力学関数$U,H,F,G$の偏微分は順番を入れ替えられる」という性質を使います。
例えば、内部エネルギー$U$を自然な変数$S,V$で表した場合、全微分は$\text{d}U=T\text{d}S-P\text{d}V$です。つまり、$\Bigl(\frac{\partial{U}}{\partial{S}}\Bigl)_V=T$、$\Bigl(\frac{\partial{U}}{\partial{V}}\Bigl)_S=-P$です。
ここで、「熱力学関数$U$の偏微分は順番を入れ替えられる($\frac{\partial^2U}{\partial{V}\partial{S}}=\frac{\partial^2U}{\partial{S}\partial{V}}$)」ので、$\Bigl\{\frac{\partial}{\partial{V}}\Bigl(\frac{\partial{U}}{\partial{S}}\Bigl)_V\Bigl\}_S=\Bigl\{\frac{\partial}{\partial{S}}\Bigl(\frac{\partial{U}}{\partial{V}}\Bigl)_S\Bigl\}_V$が利用できます。
これに$\Bigl(\frac{\partial{U}}{\partial{S}}\Bigl)_V=T$、$\Bigl(\frac{\partial{U}}{\partial{V}}\Bigl)_S=-P$を代入すると、Maxwellの関係式の1つである$\Bigl(\frac{\partial{T}}{\partial{V}}\Bigl)_S=-\Bigl(\frac{\partial{P}}{\partial{S}}\Bigl)_V$を得ることができます。
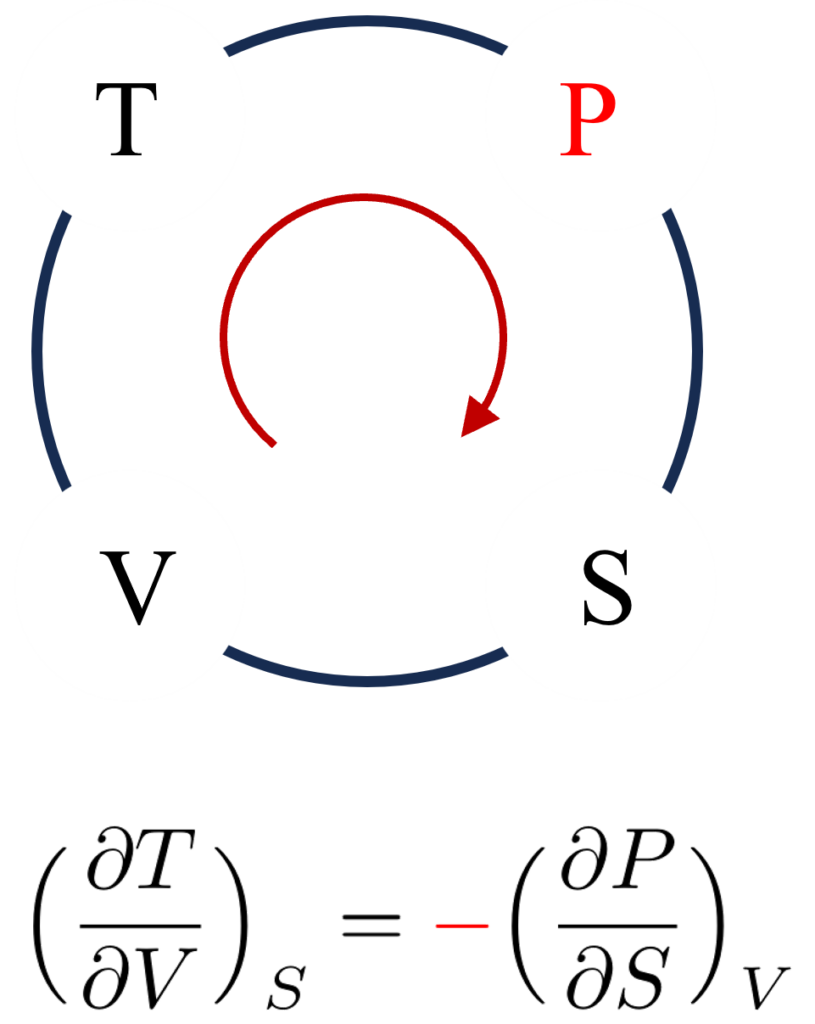

これは$P$を右上に置き、$PSVT$と時計回りに並べたときのMaxwell関係式に対応します。
ほかの3つのMaxwell関係式も同様に、それぞれ$H$、$F$、$G$の偏微分が交換可能であることを利用するとすぐに得ることができます。

試験中にプラスマイナスが不安になったら、$U,H,F,G$の全微分を利用してMaxwell関係式を確認しましょう。
まとめ
このページではマクスウェル関係式の覚え方を一つ紹介し、もし忘れてしまっても簡単にマクスウェルの関係式を作る方法を解説しました。
圧力PやエントロピーSなどの関係式が4つもあり、さらにはプラスマイナスの符号まで正確に使う必要があり、かなり覚えにくい関係式です。
テスト中、マクスウェルの関係式を忘れてしまったとしても、熱力学関数$U,H,F,G$の偏微分は順番を入れ替えられる性質を使って素早くマクスウェルの関係式を導けると安心です。

