私がランキンサイクルを初めて知ったのは、エネルギー管理士(通称:エネ管)の試験勉強をしていた時です。当時は、「水沸かして発電してるんだな」くらいの認識で、ほかのサイクルとの違いもよくわからないままでした。
ただ、よくよく調べてみると、ランキンサイクルは、水を使うことでTS線図的にカルノーサイクルに近づけている、という面白いことに気づきました。
このページでは、火力発電所の基本サイクルであるランキンサイクルの基本構成やTS線図の描き方と、エンタルピーを使った熱効率の計算を図を使ってわかりやすく解説します。
ランキンサイクル熱効率とは?基礎知識と意義をわかりやすく解説
ランキンサイクルのポイント
はじめに、ランキンサイクルを簡単に確認しましょう!
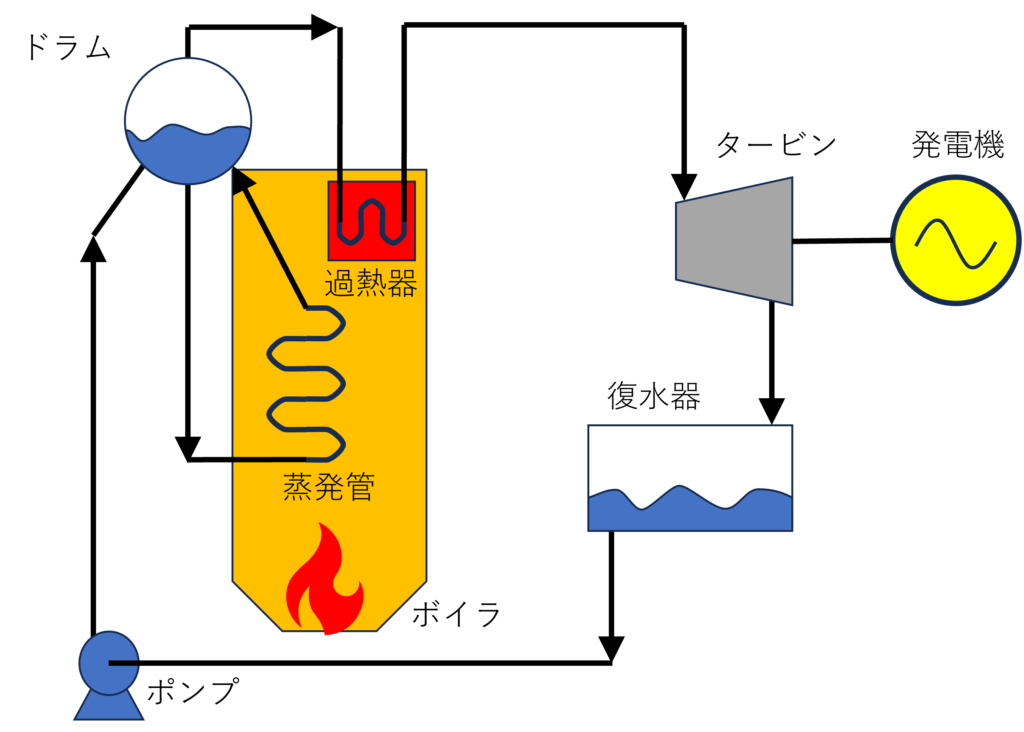
ランキンサイクルは、火力発電所で利用される熱機関サイクルです。ランキンサイクルは、ボイラで水を蒸気にして、その蒸気でタービンを回して電気を作ることが最大の目的です。

「蒸気を作ってタービンを回す」が基本的な考えだね
ランキンサイクルの重要なポイントは次の3つです。
- ランキンサイクルの作業流体は水と水蒸気
- ボイラで作った高圧の水蒸気でタービンを回して発電する
- 復水器で蒸気を凝縮させて高真空を作り、タービンからの排気を促す

「水」といっても、内部が汚れないようにCa$^{2+}$イオンや溶存O$_2$ガスの濃度は厳格に規定されます。

たしかに、水道水は蒸発させたらCaの白い粉がでてくるもんね
他の熱機関(オットーサイクル、カルノーサイクル)との違い
なぜ火力発電所ではオットーサイクルではなく、ランキンサイクルを使うのでしょうか??
大型化が可能であるといったメリットももちろんありますが、熱効率的な視点に立つと、水の相変化を使うことでオットーサイクルよりもカルノーサイクルに近づくので(TS線図でわかる)、熱効率が高いことが最大のメリットです。
| サイクル名 | 作動流体 | 主な用途 | 特徴 |
|---|---|---|---|
| ランキンサイクル | 水・蒸気 | 火力発電 | 相変化を利用 |
| オットーサイクル | 空気・燃料混合気 | 自動車エンジン | 小型化が可能 |
| カルノーサイクル | 理想気体 | 理論計算 | 最高効率 |

どうして急にTS線図の話をするの?

実はサイクルのTS線図が長方形に近づけるほど熱効率を上げられるのです。

他のページで説明している通り、TS線図を長方形(カルノーサイクル)に近づけられれば、熱効率を上げることができます。
ランキンサイクルの基本構成と流体の動き
次に、ランキンサイクルの設備を見ていきましょう!ランキンサイクルで特に重要な装置は4つ(ボイラ、タービン、復水器、ポンプ)です。

まず、水はポンプによってドラムに送られ、ボイラで加熱されて蒸気になります。この蒸気がタービンを回すことで、電気を生み出します。その後、復水器で再び水に戻り、ポンプで再びドラムへ送られることでサイクルが一回りします。
- ボイラ:水を蒸気に変える
- タービン:蒸気のエネルギーで仕事をする
- 復水器:蒸気を水に戻す
- ポンプ:水をボイラーに送り込む
たった1%でも熱効率を上げる意味がなぜあるのか
ランキンサイクルは火力発電所の熱サイクルの基本ですが、火力発電所ということで熱効率を$1\%$でも$0.1\%$でも上げることによる効果は劇大です。

実際に、火力発電所の熱効率が$1\%$上がる威力を考えてみよう。
経済産業省のHPによると、日本での2025年における火力発電所による総発電量は約600億kWhです。もし発電所の熱効率が$60\%$であったとして、効率が$1\%$だけ上がっただけでも、同じ燃料で$600$億$\times\frac{61}{60}-600$億$=10$億$\text{kWh}$分も多く発電できることになります。

10$億$\text{kWh}$分とは120万人分(京都市程度)をカバーできる電力に相当します
このように、火力発電所はわずかでも効率を上げることで一つの大都市の電力分を丸ごと賄えるくらいインパクトがあります。そのため、ランキンサイクルの熱効率のポイントを知ることは、経済的・環境的なメリットに直結します。
【図解】ランキンサイクルのT-S線図とエネルギーフロー
TS線図で見るランキンサイクルの各工程
ランキンサイクルの理解には、温度($T$)とエントロピー($S$)を軸にとったTS線図が非常に役立ちます。ランキンサイクルの工程を下のように番号付けして、TS線図に落とし込んでいきましょう。
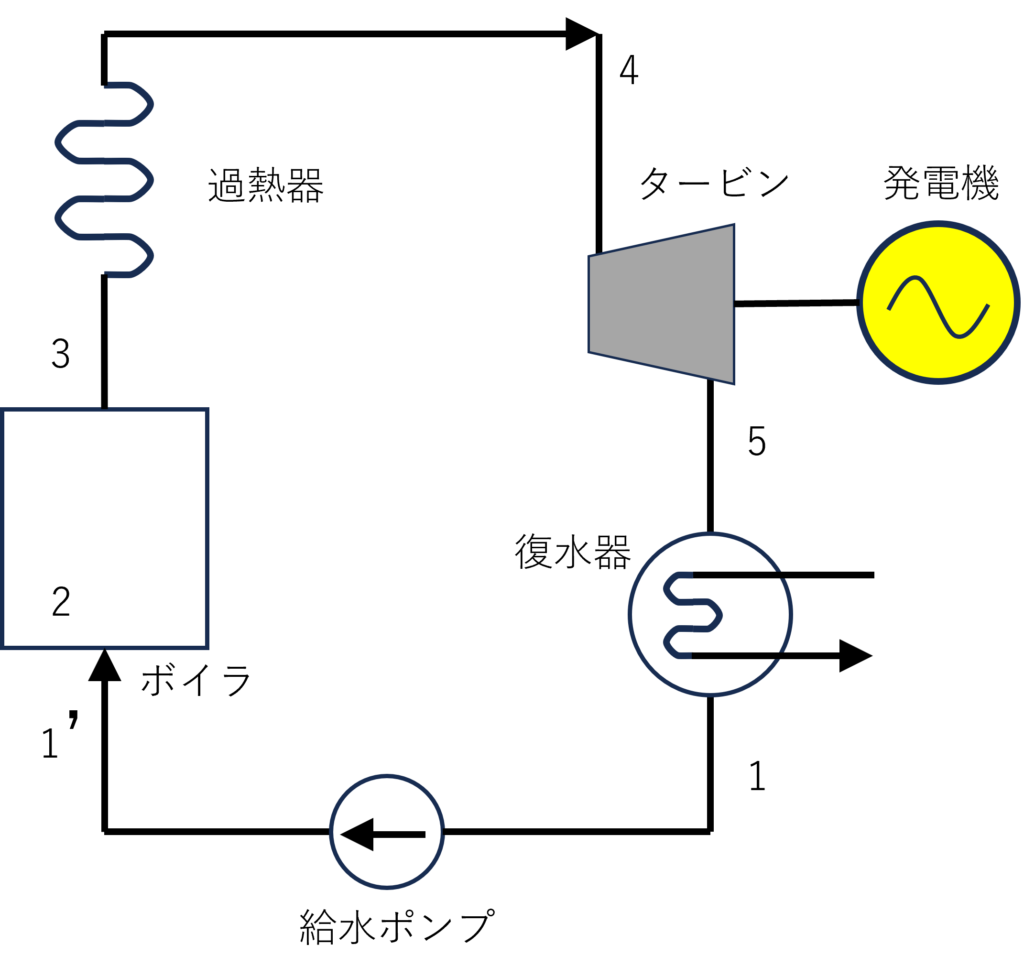
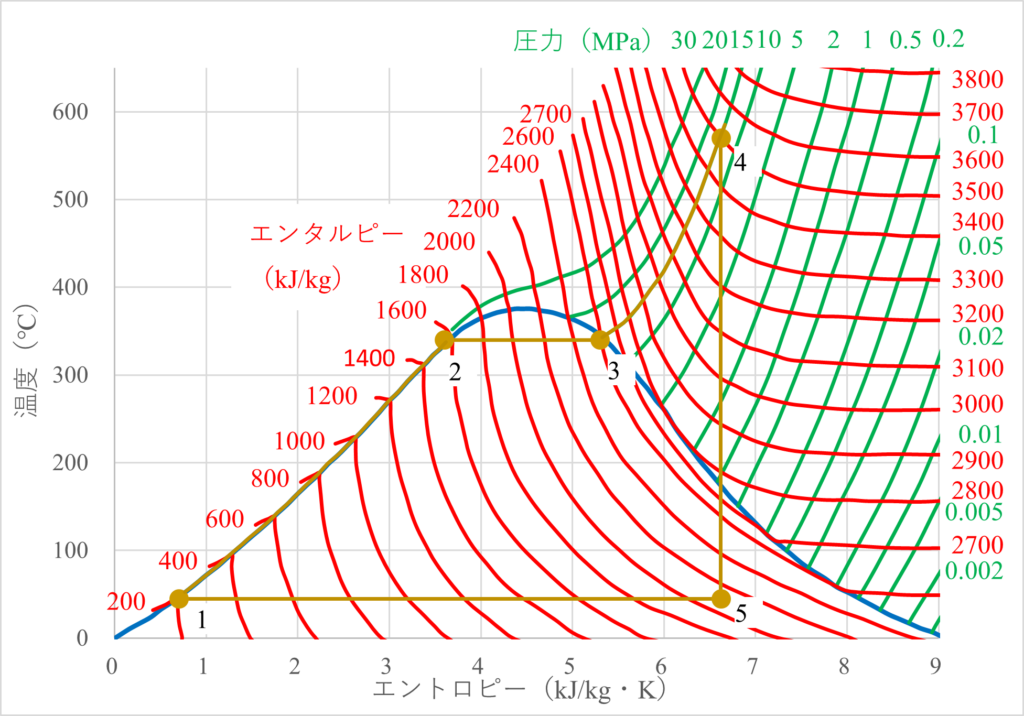
TS線図では、サイクルの各工程が視覚的に表現され、加熱・膨張・冷却・圧縮の流れが一目でわかります。例えば、$15\text{MPa}$の蒸気を利用するランキンサイクルのTS線図は下のようになります。

線が多すぎてわけわかんないよ

ご安心ください。一つずつ解説しましょう
実は、上の大量の線で描かれたTS線図によって、熱効率だけでなく、どのようにすれば熱効率を上げられるか(要するに再熱・再生サイクルやコンバインドサイクル)まで知ることができます。
このページでは、基本となるランキンサイクルのTS線図の描き方・読み方を一つずつ解説します。
水のT-S線図

では、実際にランキンサイクルのTS線図を書いてみましょう!
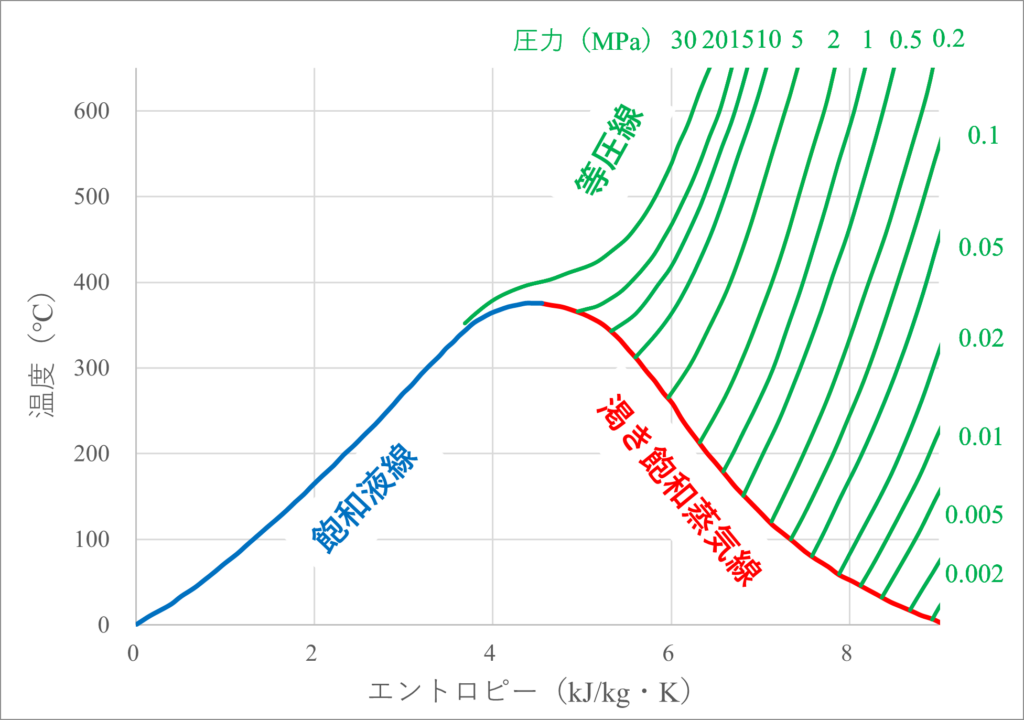
まずはランキンサイクルを書き込む水のTS線図を見てみましょう。TS線図で肝となるのは「飽和液線・蒸気線」と「等圧線」です。
ランキンサイクルでは水の蒸発と凝縮がポイントになるため「飽和液線・蒸気線」に対して各工程がどの位置関係になるかが非常に重要です。さらに、水の加熱は等圧で行われるので、ボイラーからタービンまでは等圧線に沿った動きになります。
簡単に言ってしまうと、ボイラーに入る前は水は液体なので飽和液線の左側、タービン入口では超高温高圧の蒸気になるので飽和蒸気線の右上、タービン出口では蒸気と水の混合状態になるので、飽和液線と飽和蒸気線の間にそれぞれランキンサイクルの点が来ることになりまs。
サイクルの始まり(ポンプ)の状態はどこ?
いま、ポンプ手前では水が$0.1\text{MPa}$、$45\text{C}^\circ$であったとしましょう。圧力$P$と温度$T$の2つが確定しているので、状態を特定することができ、熱力学量は全て知ることができます。今の場合エントロピー$S$は$0.7(\text{kJ/kg}\cdot\text{K})$と特定できます。

エントロピーの値は化学便覧で知ることができます
そのため、ポンプ手前や出口の状態$3$はTS線図では左下の点として落とし込むことができます。
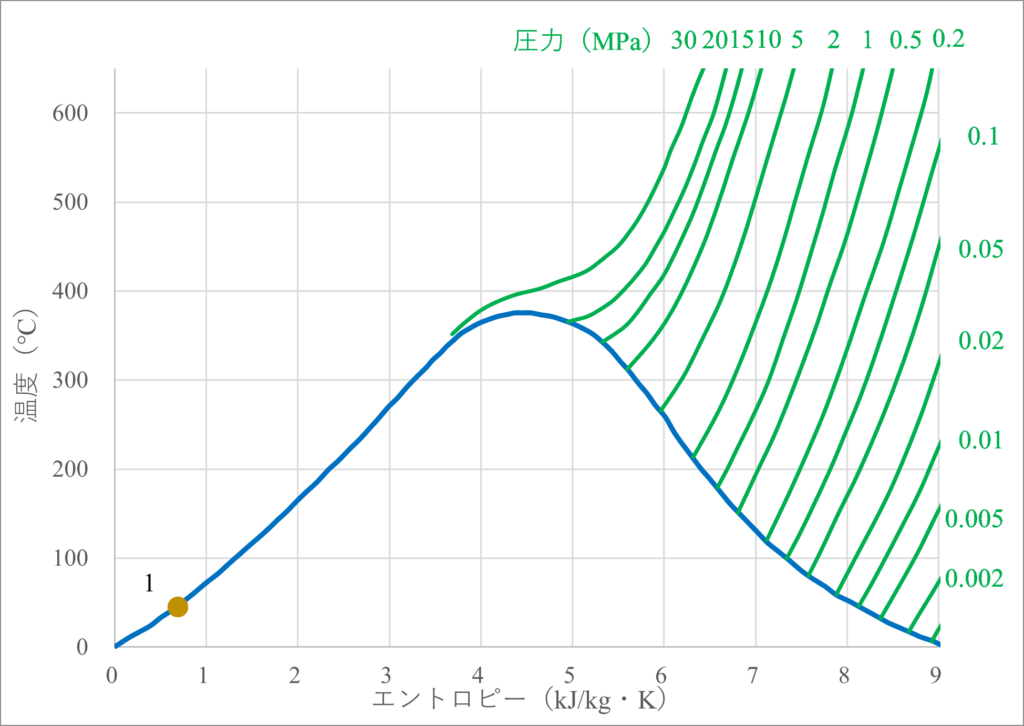

ポンプによって厳密には1の位置から右上にずれ1’となりますが、そのあとの工程に比べると些細な違いなので本ページでは1=1’とします
このページでは、送液やバルブによる圧力の変動は無視します。(ランキンサイクル全体から見ると影響はかなり小さいため)
タービン入口の状態はどこ?
ポンプ出口(1)の状態は決まりましたが、ボイラーにおける状態(4)はどうやって決まるのでしょうか?
実は、ポンプ以降はタービン入口における圧力と温度を決めると、一気にボイラーや過熱器、タービン入口の状態までTS線図に落とし込めます。

これは、圧力を決めると蒸発し始める温度や全て蒸発しきる温度が決まってしまうからです。
例えば、タービン入口での圧力を$15\text{MPa}$、温度を$570\text{C}^\circ$とすると、TS線図は1から2、3、4まで一気に決めることができます。
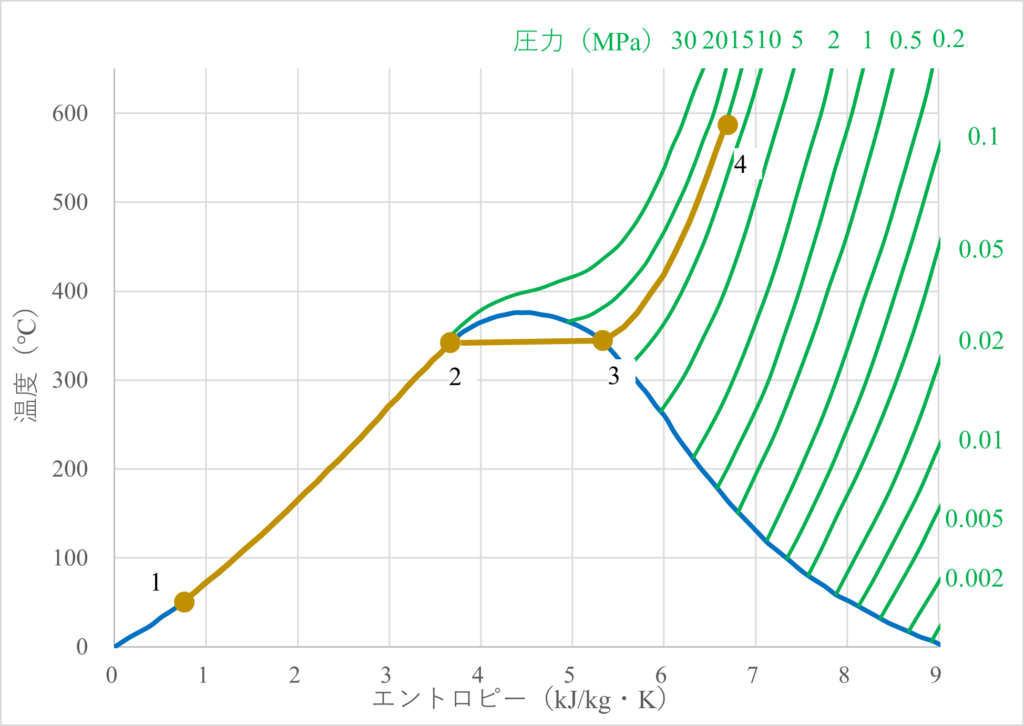

実際の火力発電所では電力需給(タービン負荷)に応じて蒸気流量をバルブ制御します(4での圧力や温度が変わる)。
タービン出口の状態はどこ?
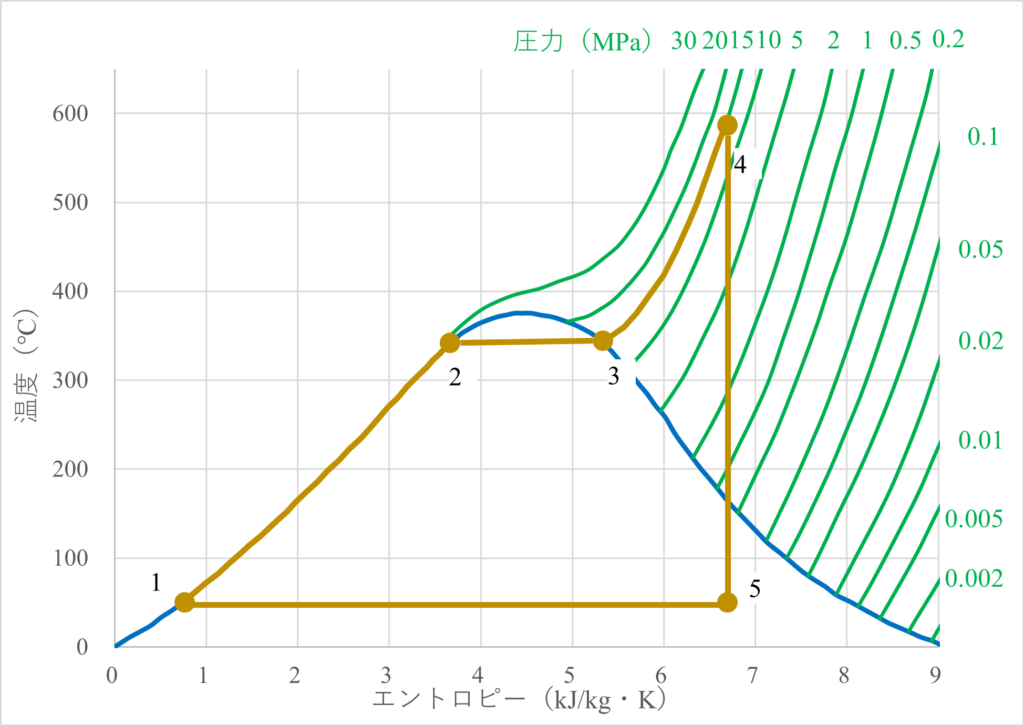
タービンに入った超高温・高圧の蒸気は羽根車に回転エネルギーを与えた後、タービン出口では湿り蒸気になっています。
さらに、タービン出口の湿り蒸気は復水器を通って完全に水になった後、再びポンプへ戻っていきます。
つまり、ポンプまでは同じ圧力なので、タービン出口での状態はタービン入口からまっすぐ下に伸ばした線とポンプからまっすぐ右に伸ばした線の交点で表すことができます。
繰り返しですが(3回目)、ガスタービンのブレイトンサイクルや内燃機関のオットーサイクルと比較したとき、水と蒸気の相変化を利用する点がやはりランキンサイクルの特徴です。

TS線図では、水⇒蒸気は2⇒3への横線で、蒸気⇒水は5⇒1への横線で表されているね。
エンタルピー線も重ね合わせると完成
ランキンサイクルの各工程をプロットできたので、後は等エンタルピー線を重ね合わせると初めにお見せしたランキンサイクルの「詳細な」TS線図を得ることができます。

ランキンサイクル熱効率の求め方:基礎公式から実践計算例まで
エネルギーの流れと仕事・熱量の関係
ランキンサイクルの熱効率($\eta$)は、ボイラーで加えた熱量($Q_\text{in}$)とタービンで得られる仕事($W_\text{out}=Q_\text{in}-Q_\text{out}$)の比で表されます。つまり、$\eta=1-Q_\text{out}/Q_\text{in}$です。
- $W_\text{out}$:タービンで得られる仕事
- $Q_\text{in}$:ボイラーで加える熱量
- $Q_\text{out}$:タービンと復水器で捨てられる熱量
実際の計算ではエンタルピー($h$)を用いて「$\eta=(h1-h2)/(h1-h4)$」のように表現されることが多いです。

状態間の吸熱量はエンタルピー差と等しいもんね
具体例:ランキンサイクル熱効率の基本的な例題
例えば、タービン入口のエンタルピーが$3500\text{kJ/kg}$、出口が$2100\text{kJ/kg}$、ポンプ入口が$200\text{kJ/kg}$の場合、熱効率は次のように計算します。

タービンでの仕事は$3500-2100=1400\text{kJ/kg}$、ポンプ、ボイラーでの入熱量は$3500-200=3300\text{kJ/kg}$なので、熱効率$\eta=1400/3300=42\%$となります。

このように、各点のエンタルピーを正確に把握することが計算のポイントです。
乾き度がランキンサイクルに与える影響
渇き度もT-S線図から分かる
ランキンサイクルでは、蒸気の入口(タービン入口)と出口(タービン出口)で温度・圧力・乾き度が大きく変化します。タービン入口では高温高圧の過熱蒸気であったも、出口では水が混じった湿り蒸気となります。
| 工程 | 温度 | 圧力 | 乾き度 |
|---|---|---|---|
| タービン入口 | 高 | 高 | 1(過熱蒸気) |
| タービン出口 | 低 | 低 | 0.8~1(湿り蒸気) |
実は、先ほどまでにプロットしたTS線図を使うと、この渇き度$x$に関してもタービンの途中や出口での値を知ることができます。
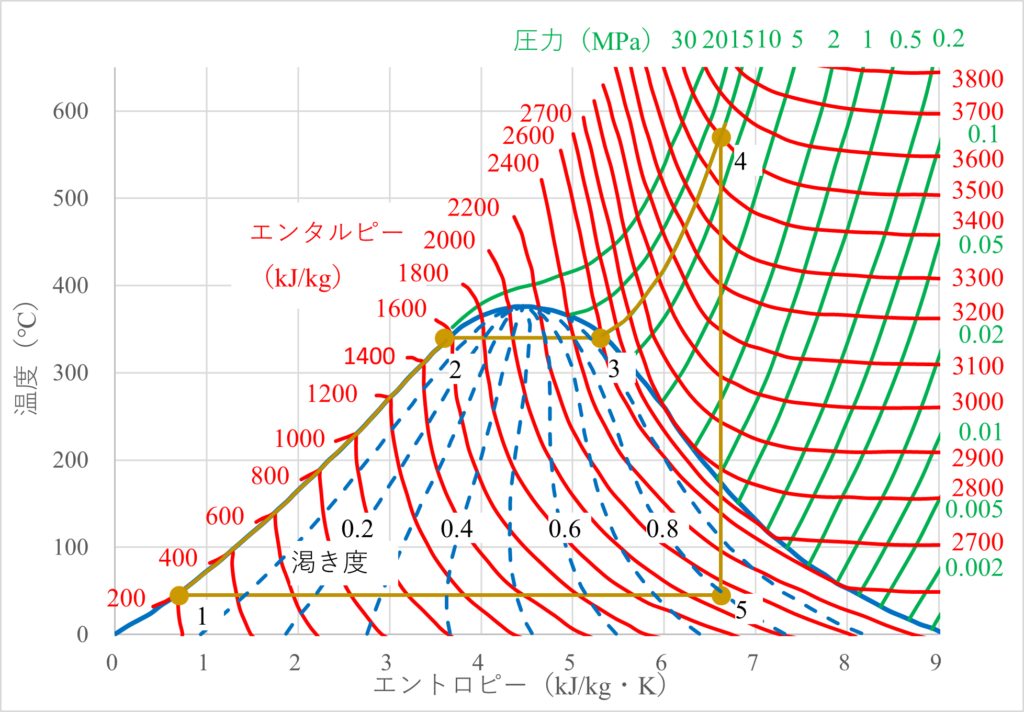

TS線図に渇き度$x$の線を重ねるだけです

今の場合だと、タービン出口で渇き度は0.8ということになるね
乾き度(蒸気中の水分割合のこと)は、熱効率やタービンの安全性に大きな影響を与えます。乾き度が低いと、蒸気中の水分が多くなり、水滴が高速でタービンにあたって効率が下がるだけでなく、タービン自信の損傷にさえつながります。
火力発電所でカルノーサイクルはなぜ無理か
発電所での基本サイクルとなるランキンサイクルですが、熱サイクルの理想形であるカルノーサイクルはなぜ採用できないのでしょうか。定圧、断熱工程のみから構成されるサイクル(1⇒2⇒3⇒4⇒1)を考えてみましょう。

無理な理由:その1
このサイクルが現実の発電所で採用できない1つ目の工程は1$\to$2の断熱膨張工程です。ここではタービンを置き、蒸気によって発電を行う必要がありますが、飽和蒸気を使用した場合、すぐに水滴がタービン上で発生します。そのため、蒸気と水滴の速度差による摩擦などによる大きな損失(湿り損失)がすぐ発生し、実際の発電には使えません。

発電所でもタービン出口付近では膨張の結果、水滴が発生します。水滴による湿り損失はタービン損失の数十%を占めます。
無理な理由:その2
さらに、実現が困難な工程は復水器における2$to$3の工程です。カルノーサイクルにするにはボイラー入口の$4$で飽和液線上に状態を持っていく必要がありますが、復水器で狙った湿り度の$3$までピンポイントで冷却することは不可能です。
無理な理由:その3
最後に、狙った湿り度まで復水器で冷却できたとして、その気液混合流体を3$\to$4まで昇圧させることは困難です。圧縮機で昇圧するには全て気体である必要がありますし、ポンプで昇圧するには全て液体である必要があるからです。

気体の混じった液体をポンプに入れるとキャビテーションが発生して、ポンプが損傷するよね
これらの観点だけでも、発電所でカルノーサイクルを実現させることは実質的に不可能です。そのため、発電所の基本的なサイクルはランキンサイクルになっています。
熱効率を高めるには?ランキンサイクル改善の技術
熱効率の理論値と実際値はなぜ異なる?

これまでは理論的な話をしてきましたが、現実で起こる損失を見てみましょう。
ランキンサイクルは理想的な条件(摩擦や熱損失がない、完全な可逆過程)で計算されますが、実際の発電所やプラントでは、配管や装置での熱損失、圧力損失、機械的損失などが避けられません。また、蒸気の乾き度や装置の経年劣化も効率低下の要因です。
発電サイクルとは別になりますが、「所内利用」といって発電所自体の設備(事務所の電気やポンプ)を稼働させるためにもタービンで作り出した電気を利用するため、発電所としての出力はさらに下がります。
ランキンサイクルの限界と改善余地はどこまであるか
しかし、ランキンサイクルにはまだまだ改善の余地があります。特に有名な方法は再熱・再生サイクルやコンバインドサイクルです。
このページでは詳細は触れませんが、「水蒸気を再び熱するのが再熱サイクル」、「使用後の蒸気の一部を別の道で再び生きかえらせるのが再生サイクル」「ボイラの排熱でもタービンを回すのがコンバインドサイクル」です。

これらの技術は要するに「ランキンサイクルのTS線図をより長方形に近づけていく」ための方法です。
まとめ
このページでは、火力発電所の基本サイクルであるランキンサイクルの基本構成やTS線図、エネルギーフローを理解し、エンタルピーを使った熱効率の計算を図を使って解説しました。
ランキンサイクルはオットーサイクル等のいろいろあるサイクルに埋もれがちですが、TS線図を活用してランキンサイクルを見てみるととても面白いものです。
普通の発電所では再熱・再生サイクルやコージェネレーションなども活用していますが、これらのサイクルもTS線図的にはランキンサイクルをより長方形に近づけていくという技術です。別のページで、これらも解説しているので、是非見てください。







